题目内容
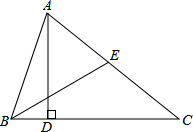 在△ABC中,AD⊥BC于D点,BE为中线,且∠CBE=30°.求证:AD=BE.
在△ABC中,AD⊥BC于D点,BE为中线,且∠CBE=30°.求证:AD=BE.考点:三角形中位线定理,含30度角的直角三角形
专题:证明题
分析:首先过点E作EF⊥BC于点F,利用已知得出EF是△ADC的中位线,再利用EF=
BE求出即可.
| 1 |
| 2 |
解答: 证明:过点E作EF⊥BC于点F,
证明:过点E作EF⊥BC于点F,
∵AD⊥BC于D点,EF⊥BC,
∴AD∥EF,
∵BE为中线,
∴F为DC的中点,
∴EF是△ADC的中位线,
∴EF=
AD,
∵∠CBE=30°,∠EFB=90°,
∴EF=
BE,
∴AD=BE.
 证明:过点E作EF⊥BC于点F,
证明:过点E作EF⊥BC于点F,∵AD⊥BC于D点,EF⊥BC,
∴AD∥EF,
∵BE为中线,
∴F为DC的中点,
∴EF是△ADC的中位线,
∴EF=
| 1 |
| 2 |
∵∠CBE=30°,∠EFB=90°,
∴EF=
| 1 |
| 2 |
∴AD=BE.
点评:此题主要考查了三角形中位线定理以及含30°角的直角三角形,得出EF是△ADC的中位线是解题关键.

练习册系列答案
相关题目
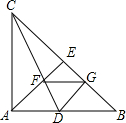 如图,△ABC中,∠ACB=90°,AE⊥BC于点E,CD平分∠ACB交AB于点D,CD、AE交于点F,FG∥AB交BC于点G,求证:四边形ADGF是菱形.
如图,△ABC中,∠ACB=90°,AE⊥BC于点E,CD平分∠ACB交AB于点D,CD、AE交于点F,FG∥AB交BC于点G,求证:四边形ADGF是菱形.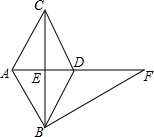 如图,BC垂直平分AD,垂足为E,AD平分∠BAC
如图,BC垂直平分AD,垂足为E,AD平分∠BAC 如图,AD平分∠BAC,∠D=∠DAB,E在AD上,BE的延长线交CD于F,连CE,且∠1=∠2,试说明AB=AC.
如图,AD平分∠BAC,∠D=∠DAB,E在AD上,BE的延长线交CD于F,连CE,且∠1=∠2,试说明AB=AC. 如图,在平行四边形ABCD中,E是BC上的3等分点,AE交BD于点F.
如图,在平行四边形ABCD中,E是BC上的3等分点,AE交BD于点F.