题目内容
在菱形ABCD中对角线AC、BD相交于点O,AB=5AC=6,过点D作AC的平行线交BC的延长线于点E,求△BDE的面积.
考点:菱形的性质
专题:
分析:先判断出四边形ACED是平行四边形,从而得出DE的长度,根据菱形的性质求出BD的长度,利用勾股定理的逆定理可得出△BDE是直角三角形,计算出面积即可.
解答:解:四边形ABCD是菱形,
∴AD∥BE,
∵AC∥DE,
∴四边形ACED是平行四边形,
∴AC=DE=6,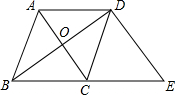
∴AO=OC=
AC=3,
在RT△BCO中,∵AB=5,
∴BO=
=4,即可得BD=8,
又∵BE=BC+CE=BC+AD=10,
∴△BDE是直角三角形,
∴S△BDE=
DE•BD=24.
∴AD∥BE,
∵AC∥DE,
∴四边形ACED是平行四边形,
∴AC=DE=6,

∴AO=OC=
| 1 |
| 2 |
在RT△BCO中,∵AB=5,
∴BO=
| AB2-AO2 |
又∵BE=BC+CE=BC+AD=10,
∴△BDE是直角三角形,
∴S△BDE=
| 1 |
| 2 |
点评:此题考查了菱形的性质、勾股定理的逆定理及三角形的面积,属于基础题,求出BD的长度,判断△BDE是直角三角形,是解答本题的关键.

练习册系列答案
相关题目
若分解因式a2+ma+
=(a-
)2,则m等于( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、-2 | B、2 | C、1 | D、-1 |
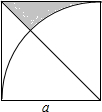 如图所示,以正方形的顶点为圆心,拉长为半径作圆弧,过这个顶点做正方形的对角线.已知正方形的边长为a,用含a的代表数式表示图中阴影部分的面积S=
如图所示,以正方形的顶点为圆心,拉长为半径作圆弧,过这个顶点做正方形的对角线.已知正方形的边长为a,用含a的代表数式表示图中阴影部分的面积S= 如图,在△ABC中,AC=BC=3,AB=3
如图,在△ABC中,AC=BC=3,AB=3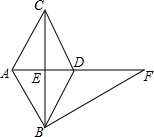 如图,BC垂直平分AD,垂足为E,AD平分∠BAC
如图,BC垂直平分AD,垂足为E,AD平分∠BAC