题目内容
5.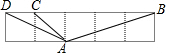 如图,5个同样大小的正方形拼成一个长方形,则∠ABC+∠ADC+∠ACB=90°.
如图,5个同样大小的正方形拼成一个长方形,则∠ABC+∠ADC+∠ACB=90°.
分析 利用勾股定理分别计算出△ACD和△ADB的各个边长,根据有三边比值相等的两三角形相似可判定△ACD和△ADB相定理即可求出似,再根据相似三角形的性质:对应角相等和三角形外角和定理即可求出∠ABC+∠ADC+∠ACB的度数.
解答 解:设每个小正方形的边长为1,
由勾股定理得:AC=$\sqrt{2}$,AD=$\sqrt{5}$,AB=$\sqrt{10}$,
又∵DC=1,BD=5,
∴$\frac{AD}{BD}=\frac{\sqrt{5}}{5}$,$\frac{AC}{AB}$=$\frac{\sqrt{5}}{5}$,$\frac{CD}{AD}$=$\frac{\sqrt{5}}{5}$,
∴$\frac{AD}{BD}=\frac{AC}{AB}=\frac{CD}{AD}$,
∴△ADC∽△BDA,
∴∠DAC=∠ABD,
∵∠ACB=45°,
∴∠ACB=∠DAC+∠ADB=45°,
∴∠ABC+∠ADC+∠ACB=90°;
故答案为:90°.
点评 本题考查了相似三角形的判定和相似三角形的性质、勾股定理的运用和三角形的外角性质;证明三角形相似是解决问题的突破口.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.下列图形中,不是轴对称图形的是( )
| A. | 正方形 | B. | 等腰直角三角形 | ||
| C. | 等边三角形 | D. | 含30°的直角三角形 |
15.如果2x2+ax-2y+7-(bx2-2x+9y-1)的值与x的取值无关,则-a-2b的值为( )
| A. | 3 | B. | 1 | C. | 2 | D. | -2 |
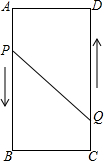 A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.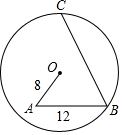 如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则⊙O的半径长为4$\sqrt{7}$.
如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则⊙O的半径长为4$\sqrt{7}$. 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014,到BC的距离记为h2015;若h1=1,则h2016的值为2-$\frac{1}{{2}^{2015}}$.
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014,到BC的距离记为h2015;若h1=1,则h2016的值为2-$\frac{1}{{2}^{2015}}$.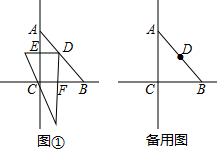
 如图,长、宽分别为a、b的长方形硬纸片拼成一个“带孔”正方形,利用面积的不同表示方法,写出一个等式(a+b)2=(a-b)2+4ab.
如图,长、宽分别为a、b的长方形硬纸片拼成一个“带孔”正方形,利用面积的不同表示方法,写出一个等式(a+b)2=(a-b)2+4ab.