题目内容
14.已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图所示).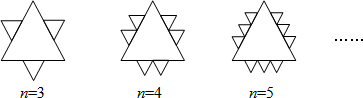
(1)当n=5时,共向外作出了9个小等边三角形,每个小等边三角形的面积为$\frac{1}{25}$;
(2)当n=k时,共向外作出了3(k-2)个小等边三角形,这些小等边三角形的面积和为$\frac{3(k-2)}{{k}^{2}}$S(用含k的式子表示).
分析 结合图形正确数出前面几个具体值,从而发现等边三角形的个数和等分点的个数之间的关系:是n等分点的时候,每条边可以作(n-2)个三角形,共有3(n-2)个三角形;再根据相似三角形面积的比是边长的比的平方进行计算.
解答 解:(1)当n=5时,共有3×(5-2)=9个小等边三角形,
∴每个小三角形与大三角形边长的比=$\frac{1}{5}$,
∵大三角形的面积是S,
∴每个小三角形的面积为$\frac{1}{25}$;‘
(2)由(1)可知,当n=k时,共有3×(k-2)=3(k-2),每个小三角形的面积为$\frac{3(k-2)}{{k}^{2}}$S.
故答案为:(1)9,$\frac{1}{25}$;(2)3(k-2),$\frac{3(k-2)}{{k}^{2}}$S.
点评 此题考查了规律型:图形的变化类,此题要特别注意画等边三角形的时候,必须以相邻等分点为顶点向外作小等边三角形,所以有n等分点的时候,一边可以作(n-2)个等边三角形;计算面积的时候,主要是根据面积比是边长的平方比进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某农科所在相同条件下做某作物种子发芽率的试验,结果如下所示:
一般地,1000kg种子中大约有100kg种子是不能发芽的.
| 种子个数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| 发芽种子个数 | 94 | 187 | 282 | 338 | 435 | 530 | 624 | 718 | 814 | 901 |
| 发芽种子频率 | 0.940 | 0.935 | 0.940 | 0.845 | 0.870 | 0.883 | 0.891 | 0.898 | 0.904 | 0.901 |
3.某商品的价格标签已丢失,售货员只知道它的进价为80元,打七折售出后,仍可获利5%,你认为标签上的价格为( )元.
| A. | 110 | B. | 120 | C. | 130 | D. | 140 |
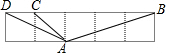 如图,5个同样大小的正方形拼成一个长方形,则∠ABC+∠ADC+∠ACB=90°.
如图,5个同样大小的正方形拼成一个长方形,则∠ABC+∠ADC+∠ACB=90°.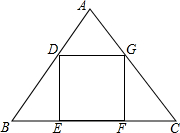 如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,已知BC=6,△ABC的面积为9,则正方形DEFG的面积为4.
如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,已知BC=6,△ABC的面积为9,则正方形DEFG的面积为4.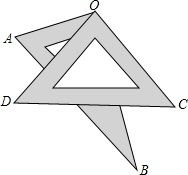 如图所示,将一副三角板重叠放在一起,使两直角顶点重合于点O
如图所示,将一副三角板重叠放在一起,使两直角顶点重合于点O