题目内容
5.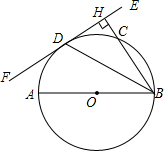 已知:如图,AB为⊙O的直径,C、D是⊙O上两点,BD平分∠ABC,BC的延长线与过点D的直线交于点H,且BH⊥DH.
已知:如图,AB为⊙O的直径,C、D是⊙O上两点,BD平分∠ABC,BC的延长线与过点D的直线交于点H,且BH⊥DH.(1)求证:DH是⊙O的切线.
(2)如果AB=10,BC=8,求圆心O到BC的距离.
分析 (1)要证DH是⊙O的切线,只要连接OD,再证OD⊥EF即可.
(2)过点O作OG⊥BC于点G,根据垂径定理求得BG,然后根据勾股定理即可求得O到BC的距离.
解答 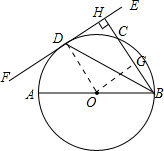 (1)证明:连接半径OD.
(1)证明:连接半径OD.
∵BD平分∠ABH,
∴∠ABD=∠HBD,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠HBD=∠ODB,
∴OD∥BH,
又∵BH⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线.
(2)解:过点O作OG⊥BC于点G,
则BG=CG=4,
在Rt△OBG中,OG=$\sqrt{O{B}^{2}-B{G}^{2}}$=$\sqrt{{5^2}-{4^2}}$=3.
点评 本题考查了切线的判定、垂径定理以及勾股定理的运用.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.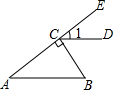 如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
 如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )| A. | 50° | B. | 40° | C. | 35° | D. | 25° |
14.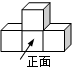 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )
 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )| A. | 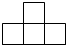 | B. |  | C. |  | D. | 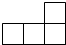 |
15.某班6名同学在一次“1分钟仰卧起坐”测试中,成绩分别为(单位:次):39,45,42,37,41,39.这组数据的众数、中位数分别是( )
| A. | 39,40 | B. | 42,37 | C. | 39,41 | D. | 41,42 |
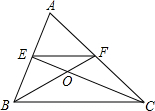 如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )
如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )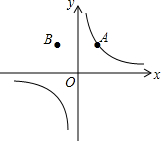 如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.
如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.