题目内容
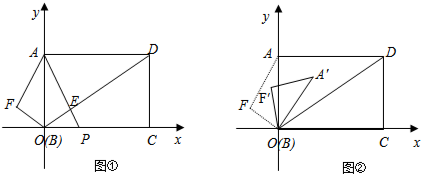
15.如图①,在直角坐标系中,矩形ABCD的顶点B与点O重合,点A的坐标为(0,5),在△AFO中,∠AFO=90°,点F的坐标为(-$\frac{12}{5}$,$\frac{9}{5}$).(1)请直接写出AF的长是4;
(2)将△AFO沿y轴对折,FO正好与矩形AOCD对角线OD在OE处重合,延长AE交x轴于P,请求出点P的坐标;
(3)如图②,将△AFO绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△AFO为△A′F′O,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线OD交于点Q.是否有这样的P、Q两点,使得DP=DQ?若有,求出此时F′Q的长.
分析 (1)根据两点间的距离公式,即可解答;
(2)根据点F与点E关于y轴对称,得到点E的坐标,利用待定系数法求出直线AE的解析式,求出与x轴的交点坐标即可解答;
(3)分两种情况解答:①点Q落在OD延长线上,PD=DQ,先证明∠3=∠Q,得到A′Q=A′O=5,根据F′Q=F′A′+A′Q,即可解答;②点Q落在OD上,且PD=DQ,证明∠A′QO=∠A′OQ,得到A′Q=A′O=5,根据F′Q=A′Q-A′F′,即可解答.
解答 解:(1)AF=$\sqrt{(\frac{12}{5})^{2}+(5-\frac{9}{5})^{2}}$=4,
故答案为:4;
(2)∵将△AFO沿y轴对折,FO正好与矩形AOCD对角线OD在OE处重合,点F的坐标为(-$\frac{12}{5}$,$\frac{9}{5}$).
∴E($\frac{12}{5}$,$\frac{9}{5}$),
设直线AE的解析式为y=kx+b,
把点A的坐标为(0,5),E($\frac{12}{5}$,$\frac{9}{5}$)代入得:$\left\{\begin{array}{l}{b=5}\\{\frac{12}{5}k+b=\frac{9}{5}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=5}\end{array}\right.$,
AE直线解析式:y=$-\frac{4}{3}x+5$,
当y=0时,$-\frac{4}{3}x+5=0$,
解得:x=$\frac{15}{4}$,
∴P($\frac{15}{4}$,0).
(3)有,
①如图③,点Q落在OD延长线上,PD=DQ,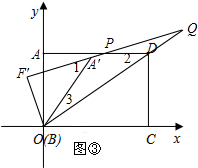
∴∠Q=∠QPD,
∴∠2=2∠Q,
∵∠1=∠3+∠Q,∠1=∠2,
∴∠3=∠Q,
∴A′Q=A′O=5,
∴F′Q=F′A′+A′Q=4+5=9.
②如图④,点Q落在OD上,且PD=DQ,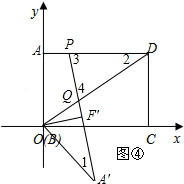
∴∠3=∠4.
∵∠2+∠3+∠4=180°,∠3=∠4,
∴∠4=90°-$\frac{1}{2}$∠2.
∵∠1=∠2,
∴∠4=90°-$\frac{1}{2}$∠1.
∴∠A′QO=∠4=90°-$\frac{1}{2}$∠1,
∴∠A′OQ=180°-∠A′QO-∠1=90°-$\frac{1}{2}$∠1,
∴∠A′QO=∠A′OQ,
∴A′Q=A′O=5,
∴F′Q=A′Q-A′F′=5-4=1.
点评 本题考查了旋转的性质、矩形的性质、等腰三角形的性质、解决本题的关键是利用待定系数法求函数的解析式以及分类讨论思想的应用,在(3)中画出图形非常重要.

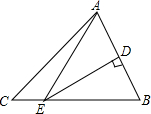 如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
| A. | (3x-y)(3x-y)=9x2-y2 | B. | (-x+y)(-x-y)=x2-y2 | C. | (x+9)(x-9)=x2-9 | D. | (x-1)2=x2-2x-1 |
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 3 | 4 | 3 | 2 |
| A. | 4 | B. | 1.65 | C. | 1.70 | D. | 3 |
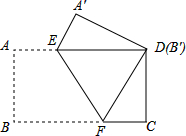 把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.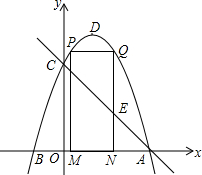 如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.
如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.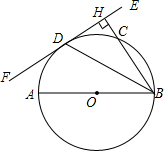 已知:如图,AB为⊙O的直径,C、D是⊙O上两点,BD平分∠ABC,BC的延长线与过点D的直线交于点H,且BH⊥DH.
已知:如图,AB为⊙O的直径,C、D是⊙O上两点,BD平分∠ABC,BC的延长线与过点D的直线交于点H,且BH⊥DH.