题目内容
实数a为 时,方程组
的解满足xy<0.
|
考点:二元一次方程组的解
专题:
分析:先把②×a再与①进行相减得出y的值,再用①×(a+1)和②×2进行相减得出x的值,最后根据xy<0,求出a的值.
解答:解:
,
②×a得:ax+a(a+1)y=a2+3a,③
③-①得:[a(a+1)-2]y=a2+3a-a,
y=
=
,
①×(a+1)得:a(a+1)x+2(a+1)y=a(a+1)④,
②×2得:2x+2(a+1)y=2a+6,⑤
④-⑤得:[a(a+1)-2]x=a(a+1)-2a-6,
x=
,
∵xy<0,
∴
•
<0,
即
<0,
∴
,解得:0<a<3,
或
,无解,
∴实数a为0<a<3时,方程组
的解满足xy<0;
故答案为:0<a<3.
|
②×a得:ax+a(a+1)y=a2+3a,③
③-①得:[a(a+1)-2]y=a2+3a-a,
y=
| a2+3a-a |
| a(a+1)-2 |
| a(a+2) |
| a2+a -2 |
①×(a+1)得:a(a+1)x+2(a+1)y=a(a+1)④,
②×2得:2x+2(a+1)y=2a+6,⑤
④-⑤得:[a(a+1)-2]x=a(a+1)-2a-6,
x=
| a2+a-2 |
| a2-a- 6 |
∵xy<0,
∴
| a2+a-2 |
| a2-a- 6 |
| a(a+2) |
| a2+a -2 |
即
| a |
| a-3 |
∴
|
或
|
∴实数a为0<a<3时,方程组
|
故答案为:0<a<3.
点评:本题考查的是解二元一次方程组,解答本题的关键是用a表示出x和y的值,再进行解答,此题难度不大.

练习册系列答案
相关题目
已知函数y=(a-2)x-3a-1,当自变量x的取值范围是3≤x≤5时,y既能达到大于5的值,又能取到小于3的值,则实数a的取值范围是( )
| A、a<3 | B、a>5 |
| C、a>8 | D、任意实数 |
 如图,一张半径为1的圆形纸片在边长为4的正方形内任意移动,则在该正方形内,这张圆形纸片“能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为4的正方形内任意移动,则在该正方形内,这张圆形纸片“能接触到的部分”的面积是( )| A、4-π | ||
| B、π | ||
| C、12+π | ||
D、15+
|
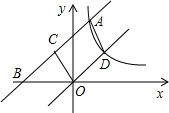 如图,直线y=x+3交反比例函数
如图,直线y=x+3交反比例函数 这个直方图回答下面的问题:
这个直方图回答下面的问题: 如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是
如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是