题目内容
 如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是
如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是考点:轴对称-最短路线问题
专题:
分析:延长DC到D',使CD=CD',G对应位置为G',则FG=FG',作D'A'⊥CD',D'A'=DA,H对应的位置为H',则G'H'=GH,再作A'B'⊥D'A',E的对应位置为E',则H'E'=HE.由两点之间线段最短可知当E、F、G'、H'、E'在一条直线上时路程最小,再延长AB至K使BK=AB,连接E′K,利用勾股定理即可求出EE′的长.
解答:解:延长DC到D',使CD=CD',G对应位置为G',则FG=FG',
同样作D'A'⊥CD',D'A'=DA,H对应的位置为H',则G'H'=GH,
再作A'B'⊥D'A',E的对应位置为E',
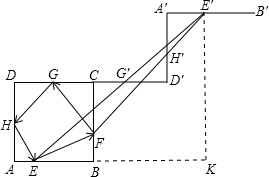
则H'E'=HE.
容易看出,当E、F、G'、H'、E'在一条直线上时路程最小,
最小路程为EE'=
=
=2
,
故答案为:2
.
同样作D'A'⊥CD',D'A'=DA,H对应的位置为H',则G'H'=GH,
再作A'B'⊥D'A',E的对应位置为E',

则H'E'=HE.
容易看出,当E、F、G'、H'、E'在一条直线上时路程最小,
最小路程为EE'=
| (2AB) 2+(2BC) 2 |
| 4+4 |
| 2 |
故答案为:2
| 2 |
点评:本题考查的是最短路线问题,解答此题的关键是画出图形,根据正方形的性质和轴对称的性质以及垂直平分线性质定理和两点之间线段最短的道理求解.

练习册系列答案
相关题目
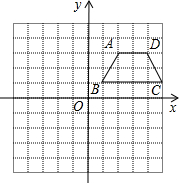 如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(2,3)、B(1,1),C(5,1),D(4,3).若将四边形ABCD绕点(1,-1)逆时针旋转90°,则D点的对应点D′的坐标为( )
如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(2,3)、B(1,1),C(5,1),D(4,3).若将四边形ABCD绕点(1,-1)逆时针旋转90°,则D点的对应点D′的坐标为( )| A、(-3,2) |
| B、(-2,3) |
| C、(-5,-4) |
| D、(-4,3) |
在平面直角坐标系中,点(9π,-5)位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
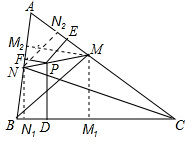 为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.
为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.
 如图,在Rt△ABC中,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,求△AEF面积最大为
如图,在Rt△ABC中,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,求△AEF面积最大为