题目内容
已知x1,x2是关于x的一元二次方程x2+(3a-1)x+2a2-1=0的两个实数根,其满足(3x1-x2)(x1-3x2)=-80.求实数a的所有可能值.
考点:根与系数的关系,根的判别式
专题:计算题
分析:根据△的意义由一元二次方程x2+(3a-1)x+2a2-1=0的两个实数根得到△≥0,即(3a-1)2-4(2a2-1)=a2-6a+5≥0,根据根与系数的关系得到x1+x2=-(3a-1),x1•x2=2a2-1,由(3x1-x2)(x1-3x2)=-80变形得到3(x1+x2)2-16x1x2=-80,于是有3(3a-1)2-16(2a2-1)=-80,解方程得到a=3或a=-
,然后代入△验算即可得到实数a的值.
| 33 |
| 5 |
解答:解:∵x1,x2是关于x的一元二次方程x2+(3a-1)x+2a2-1=0的两个实数根,
∴△≥0,即(3a-1)2-4(2a2-1)=a2-6a+5≥0
所以a≥5或a≤1.…(3分)
∴x1+x2=-(3a-1),x1•x2=2a2-1,
∵(3x1-x2)(x1-3x2)=-80,即3(x12+x22)-10x1x2=-80,
∴3(x1+x2)2-16x1x2=-80,
∴3(3a-1)2-16(2a2-1)=-80,
整理得,5a2+18a-99=0,
∴(5a+33)(a-3)=0,解得a=3或a=-
,
当a=3时,△=9-6×3+5=-4<0,故舍去,
当a=-
时,△=(-
)2-6×(-
)+6=(
)2+6×
+6>0,
∴实数a的值为-
∴△≥0,即(3a-1)2-4(2a2-1)=a2-6a+5≥0
所以a≥5或a≤1.…(3分)
∴x1+x2=-(3a-1),x1•x2=2a2-1,
∵(3x1-x2)(x1-3x2)=-80,即3(x12+x22)-10x1x2=-80,
∴3(x1+x2)2-16x1x2=-80,
∴3(3a-1)2-16(2a2-1)=-80,
整理得,5a2+18a-99=0,
∴(5a+33)(a-3)=0,解得a=3或a=-
| 33 |
| 5 |
当a=3时,△=9-6×3+5=-4<0,故舍去,
当a=-
| 33 |
| 5 |
| 33 |
| 5 |
| 33 |
| 5 |
| 33 |
| 5 |
| 33 |
| 5 |
∴实数a的值为-
| 33 |
| 5 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:如果方程的两根为x1,x2,则x1+x2=-
,x1•x2=
.也考查了一元二次方程根的判别式以及代数式的变形能力.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
已知⊙O1和⊙O2的半径分别为6和2,O1O2=3,则⊙O1和⊙O2的位置关系是( )
| A、相交 | B、外离 | C、内含 | D、内切 |
 如图,正△ABC内接于⊙O,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC=( )
如图,正△ABC内接于⊙O,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC=( )| A、60° | B、30° |
| C、90° | D、120° |
 如图,在Rt△ABC中,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,求△AEF面积最大为
如图,在Rt△ABC中,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,求△AEF面积最大为 如图,AB为⊙O的直径,半径OC⊥AB,D为AB延长线上一点,过D作⊙O的切线,E为切点,连CE交AB于F.
如图,AB为⊙O的直径,半径OC⊥AB,D为AB延长线上一点,过D作⊙O的切线,E为切点,连CE交AB于F.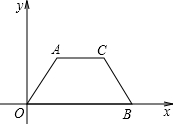 如图所示,梯形AOBC中,AC∥OB,AO=CB,A(2,2
如图所示,梯形AOBC中,AC∥OB,AO=CB,A(2,2