题目内容
1.若函数y=mx2-(m-3)x-4的图象与x轴只有一个交点,则m的值为( )| A. | 0 | B. | 1或9 | C. | -1或-9 | D. | 0或-1或-9 |
分析 分m≠0,m=0两种情况讨论,进而求出m的值得出答案即可.
解答 解:①当m=0,则函数y=mx2-(m-3)x-4是一次函数关系,故图象一定x轴有一个交点,
②当m≠0,
∵y=mx2-(m-3)x-4的图象与x轴只有一个交点,
∴b2-4ac=[-(m-3)]2-4m×(-4)=0,
解得:m1=-1,m2=,9,
综上所述:m=0或-1或-9.
故选:D.
点评 此题主要考查了抛物线与x轴交点问题,利用分类讨论得出是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
16.已知α、β是一元二次方程x2-2x-3=0的两个根,则α+β的值是( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
11. 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 包 | D. | 头 |
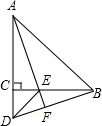 如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.
如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.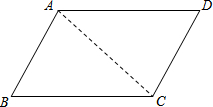 我们规定,两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD,小明同学通过测量得,AB=CD,BC=AD.
我们规定,两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD,小明同学通过测量得,AB=CD,BC=AD.
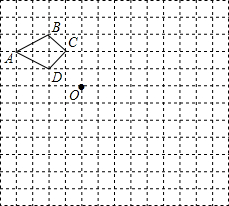 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网络线的交点)和点O,按要求画出四边形A1B1C1D1和四边形A2B2C2D2.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网络线的交点)和点O,按要求画出四边形A1B1C1D1和四边形A2B2C2D2. 把一块矩形直尺与一块直角三角板如图放置,若∠1=40°,则∠2的度数为130°.
把一块矩形直尺与一块直角三角板如图放置,若∠1=40°,则∠2的度数为130°.