题目内容
20.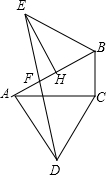 已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,以AC为边作等边△ACD,并作斜边AB的垂直平分线EH,且EB=AB,联结DE交AB于点F,求证:EF=DF.
已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,以AC为边作等边△ACD,并作斜边AB的垂直平分线EH,且EB=AB,联结DE交AB于点F,求证:EF=DF.
分析 根据直角三角形性质和线段垂直平分线求出BC=$\frac{1}{2}$AB,BH=$\frac{1}{2}$AB,推出BC=BH,推出Rt△ACB≌Rt△EHB,根据全等得出EH=AC,求出EH=AD,∠CAD=60°,∠BAD=90°,根据AAS推出△EHF≌△DAF,根据全等三角形的性质得出即可.
解答 证明:∵在Rt△ABC中,∠BAC=30°,
∴BC=$\frac{1}{2}$AB,
∵EH垂直平分AB,
∴BH=$\frac{1}{2}$AB,
∴BC=BH,
在Rt△ACB和Rt△EHB中,
$\left\{\begin{array}{l}BC=BH\\ EB=AB\end{array}\right.$,
∴Rt△ACB≌Rt△EHB(HL),
∴EH=AC,
∵等边△ACD中,AC=AD,
∴EH=AD,∠CAD=60°,∠BAD=60°+30°=90°,
在△EHF和△DAF中,
$\left\{\begin{array}{l}EH=AD\\∠EHF=∠DAF\\∠EFH=∠DFA\end{array}\right.$,
∴△EHF≌△DAF (AAS)
∴EF=DF.
点评 本题考查了线段垂直平分线性质,等边三角形的性质,含30度角的直角三角形的性质,全等三角形的性质和判定的应用,能综合运用性质进行推理是解此题的关键,难度适中.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
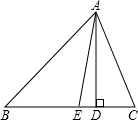 已知:如图,△ABC中,AD是高,AE平分∠BAC,∠B=50°,∠C=80°.求∠DAE的度数.
已知:如图,△ABC中,AD是高,AE平分∠BAC,∠B=50°,∠C=80°.求∠DAE的度数.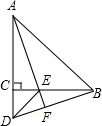 如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.
如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.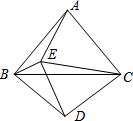 如图.△ABC与△CDE均是等边三角形,若∠DBE=76°,则∠AEB的度数是136°.
如图.△ABC与△CDE均是等边三角形,若∠DBE=76°,则∠AEB的度数是136°.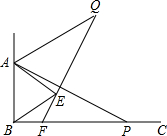 如图,已知∠ABC=90°,∠ABE是等边三角形,点P为射线BC上一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.
如图,已知∠ABC=90°,∠ABE是等边三角形,点P为射线BC上一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.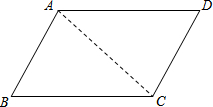 我们规定,两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD,小明同学通过测量得,AB=CD,BC=AD.
我们规定,两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD,小明同学通过测量得,AB=CD,BC=AD.