题目内容
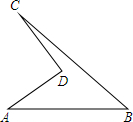
19. 已知,如图,在△ABC中,AB=AC,∠ABC=∠ACB,D是AB的中点,DE⊥AB交AC于E,若∠BEC=∠C.
已知,如图,在△ABC中,AB=AC,∠ABC=∠ACB,D是AB的中点,DE⊥AB交AC于E,若∠BEC=∠C.(1)若BE平分∠ABC,求∠A的度数;
(2)若△ABC的周长为10,△BCE的周长为6,求BC的长度.
分析 (1)设∠A的度数为x,根据等腰三角形的性质和线段垂直平分线的性质用x表示出∠ABC和∠C,根据三角形内角和定理列出算式求出x的值即可;
(2)根据线段垂直平分线的性质和三角形周长公式计算即可.
解答 解:(1)设∠A的度数为x,
∵D是AB的中点,DE⊥AB,
∴EA=EB,
∴∠ABE=∠A=x,
∵BE平分∠ABC,
∴∠ABE=∠CBE=x,
∵∠BEC=∠ABE+∠A=2x,
∴∠C=2x,
∴x+2x+2x=180°,
∴∠A=x=36°;
(2)∵△ABC的周长为10,
∴AB+AC+BC=10,
∵△BCE的周长为6,
∴BE+EC+BC=6,即AC+BC=6,
∴AB=4,
则BC=2.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.一个多边形的内角和是1440°,它是一个几边形( )
| A. | 八边形 | B. | 九边形 | C. | 十边形 | D. | 十一边形 |
10.下列说法错误的是( )
| A. | 若$\frac{x}{a}=\frac{y}{a}$,则x=y | B. | 若x2=y2,则-4x2=-4y2 | ||
| C. | 若-$\frac{1}{4}$x=6,则x=-$\frac{3}{2}$ | D. | 若6=-x,则x=-6 |
14.若a,b,c分别为三角形的三边,化简:|a-b-c|-|a-b+c|得( )
| A. | -2c | B. | 2b-2a | C. | 2a | D. | 2c-2a |
9.从正方形的铁皮上,截去2cm宽的一条长方形,余下的长方形面积是48cm2,则原来的正方形铁皮的面积是( )
| A. | 68cm2 | B. | 64cm2 | C. | 9cm2 | D. | 8cm2 |
 实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,若每平方米草皮需要300元,学校需要投入多少资金买草皮?
实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,若每平方米草皮需要300元,学校需要投入多少资金买草皮?