题目内容
2. 如图,在平面直角坐标系xOy中,已知A(9,0)、B(9,12),点M、N分别是线段OB、AB上的动点,速度分别是每秒$\frac{5}{3}$单位、2个单位,作MH⊥OA于H.现点M、N分别从点O、A同时出发,当其中一点到达端点时,另一个点也随之停止运动,设运动时间为t秒(t≥0).
如图,在平面直角坐标系xOy中,已知A(9,0)、B(9,12),点M、N分别是线段OB、AB上的动点,速度分别是每秒$\frac{5}{3}$单位、2个单位,作MH⊥OA于H.现点M、N分别从点O、A同时出发,当其中一点到达端点时,另一个点也随之停止运动,设运动时间为t秒(t≥0).(1)是否存在t的值,使四边形BMHN为平行四边形?若存在,求出t的值;若不存在,说明理由:
(2)是否存在t的值,使△OMH与以点A、N、H为顶点的三角形相似?若存在,求出t的值;若不存在,说明理由;
(3)是否存在t的值,使四边形BMHN为菱形?若存在,求出t的值;若不存在,请探究将点N的速度改变为何值时(匀速运动),能使四边形BMHN在某一时刻为菱形.
分析 根据题意证明MH∥BA,根据平行线分线段成比例定理用t表示出OH和MH,
(1)根据对边平行且相等的四边形是平行四边形列式求出t;
(2)从△OMH∽△HNA和△OMH∽△NAH两种情况进行解答,
(3)根据邻边相等的平行四边形是菱形进行分析解答即可.
解答 解:∵A(9,0)、B(9,12),
∴OA=9,AB=12,由勾股定理,OB=15,
由题意得,BA⊥OA,又MH⊥OA,
∴MH∥BA,
∴$\frac{OH}{OA}$=$\frac{MH}{AB}$=$\frac{OM}{OB}$,又OM=$\frac{5}{3}$t,
∴OH=t,MH=$\frac{4}{3}$t,
(1)使四边形BMHN为平行四边形,MH=BN即可,
即$\frac{4}{3}$t=12-2t,
解得,t=3.6;
(2)当△OMH∽△HNA时,$\frac{OH}{HA}$=$\frac{MH}{NA}$,
即$\frac{t}{9-t}$=$\frac{\frac{4}{3}t}{2t}$,解得,t=3.6;
当△OMH∽△NHA时,$\frac{OM}{NA}$=$\frac{MH}{HA}$,
即$\frac{t}{2t}$=$\frac{\frac{4}{3}t}{9-t}$,解得,t=$\frac{27}{11}$;
(3)四边形BMHN不是菱形,
由(1)得,t=3.6时,四边形BMHN为平行四边形,
此时,MH=4.8,MB=15-$\frac{5}{3}$t=9,
∴MH≠MB,四边形BMHN不是菱形,
若四边形BMHN是菱形,则HM=MB=BN,
设点N的速度改变为x,
即$\frac{4}{3}$t=15-$\frac{5}{3}$t=12-xt,
解得,t=5,x=$\frac{16}{15}$,
当点N的速度改变为$\frac{16}{15}$时,5秒四边形BMHN为菱形.
点评 本题考查的是平行四边形和菱形的判定,掌握平行四边形和菱形的判定定理是解题的关键,注意相似三角形的性质定理的运用和分类讨论思想的正确运用.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案| A. | 同位角相等,两直线平行 | B. | 如果a∥b,a∥c,那么b∥c | ||
| C. | 两直线平行,同位角相等 | D. | 相等的角是对顶角 |
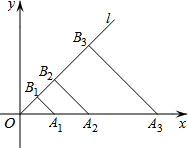 如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn-1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是(1,1),B3的坐标是(4,4),Bn的坐标是(2n-1,2n-1).
如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn-1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是(1,1),B3的坐标是(4,4),Bn的坐标是(2n-1,2n-1).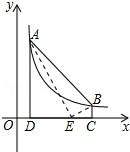 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.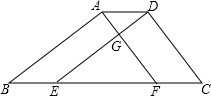 如图,四边形ABED与四边形AFCD都是平行四边形,AF和DE相交成直角,AG=3cm,DG=4cm,?ABCD的面积为36cm2,求四边形ABCD的周长.
如图,四边形ABED与四边形AFCD都是平行四边形,AF和DE相交成直角,AG=3cm,DG=4cm,?ABCD的面积为36cm2,求四边形ABCD的周长.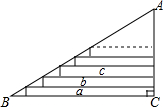 如图,在△ABC中,已知∠C=90°,AC=60,AB=100,a,b,c…是在△ABC内部的矩形,它们的一个顶点在AB上,一组对边分别在AC上或与AC平行,另一组对边分别在BC上或与BC平行.若各矩形在AC上的边长相等,矩形a的一边长是72,则这样的矩形a、b、c…的个数是( )
如图,在△ABC中,已知∠C=90°,AC=60,AB=100,a,b,c…是在△ABC内部的矩形,它们的一个顶点在AB上,一组对边分别在AC上或与AC平行,另一组对边分别在BC上或与BC平行.若各矩形在AC上的边长相等,矩形a的一边长是72,则这样的矩形a、b、c…的个数是( )