题目内容
20. 如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,则阴影部分的面积为4.
如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,则阴影部分的面积为4.
分析 根据旋转的性质得到BC≌△A1BC1,A1B=AB=4,所以△A1BA是等腰三角形,∠A1BA=30°,然后得到等腰三角形的面积,由图形可以知道S阴影=S△A1BA+S△A1BC1-S△ABC=S△A1BA,最终得到阴影部分的面积.
解答 解:∵在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,
∴△ABC≌△A1BC1,
∴A1B=AB=4,
∴△A1BA是等腰三角形,∠A1BA=30°,
∴S△A1BA=$\frac{1}{2}$×4×2=4,
又∵S阴影=S△A1BA+S△A1BC1-S△ABC,
S△A1BC1=S△ABC,
∴S阴影=S△A1BA=4.
故答案为:4.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.运用面积的和差解决不规则图形的面积是解决此题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
8.一组数据1,2,3,4,5的方差为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
15.从标有号数1到100的100张卡片中,随意抽取一张,其号数为3的倍数的概率是( )
| A. | $\frac{33}{100}$ | B. | $\frac{34}{100}$ | C. | $\frac{3}{10}$ | D. | 无法确定 |
5.下列命题正确的是( )
| A. | 一组对边相等,另一组对边平行的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
9.下列运算中,正确的是( )
| A. | x3+x=x4 | B. | (x2)3=x6 | C. | 3x-2x=-1 | D. | (a-b)2=a2-b2 |
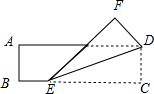 将一张长方形纸片ABCD按如图所示折叠,使顶点C落在点F处,已知AB=2,∠DEF=30°,则折痕DE的长度为( )
将一张长方形纸片ABCD按如图所示折叠,使顶点C落在点F处,已知AB=2,∠DEF=30°,则折痕DE的长度为( )