题目内容
11．
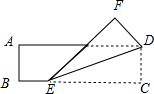将一张长方形纸片ABCD按如图所示折叠，使顶点C落在点F处，已知AB=2，∠DEF=30°，则折痕DE的长度为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 由长方形的性质和翻折的性质可得到DF=2，然后依据含30°直角三角形的性质求解即可．
解答 解：∵四边形ABCD为矩形，
∴AB=CD=2．
由翻折的性质可知：DF=DC=2，∠F=∠C=90°．
∵在Rt△EFD中，∠F=90°，∠DEF=30°，DF=2，
∴DE=2DF=2×2=4．
故选：D．
点评 本题主要考查的是翻折的性质、含30°直角三角形的性质，求得DF的长度以及ED与DF的关系是解题的关键．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
如图所示，矩形ABCD中，AB=8，AD=6，沿EF折叠，点B恰好与点D重合，点C落在点G处，求折痕EF的长度．
如图，⊙O的半径为6，AB是⊙O的弦，将线段BA绕点A逆时针旋转90°得到线段CA，当点A固定，点B在圆上运动时，则线段OC长度的最小值为6$\sqrt{2}$-6．
19．估计二次根式$\sqrt{3}$在整数（ ）
| A． | 0与1之间 | B． | 1与2之间 | C． | 2与3之间 | D． | 3与4之间 |
某市有A、B、C、D四个大型超市，分别位于一条东西走向的平安大路两侧，如图，若C（-2，8）、D（0，0），请建立适当的直角坐标系，并写出A、B两个超市相应的坐标．
16．若$\sqrt{1-2x}$有意义，则x的取值范围（ ）
| A． | x＞2 | B． | x≤$\frac{1}{2}$ | C． | x≠$\frac{1}{2}$ | D． | x≤2 |
3．已知（x-2y-1）2+|2x+y-7|=0，则3x-y=（ ）
| A． | 3 | B． | 1 | C． | 8 | D． | -6 |
20．
如图，下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是（ ）
如图，下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是（ ）| A． | ①、② | B． | ①、②、④ | C． | ②、③、④ | D． | ①、②、③、④ |
如图，在△ABC中，AB=4，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分的面积为4．