题目内容
8.若a•b≠1,且有2a2+5a+1=0,b2+5b+2=0,则$\sqrt{ab}$+$\frac{1}{\sqrt{ab}}$的值为5.分析 根据条件发现a、$\frac{1}{b}$是方程x2+5x+1=0的两根,则a+$\frac{1}{b}$=-5,$\frac{a}{b}=1$,由此即可解决问题.
解答 解:∵2a2+5a+1=0,b2+5b+2=0,
∴2a2+5a+1=0,2($\frac{1}{b}$)2+5•$\frac{1}{b}$+1=0,
∵a•b≠1,∴a≠$\frac{1}{b}$,
∴a、$\frac{1}{b}$是方程x2+5x+1=0的两根,
∴a+$\frac{1}{b}$=-5,$\frac{a}{b}$=1,
∴a=b,a<0,b<0,a+$\frac{1}{a}$=-5,
∴$\sqrt{ab}$+$\frac{1}{\sqrt{ab}}$=-a-$\frac{1}{a}$=5,
故答案为5.
点评 考查根与系数关系、整体代入的思想,解题的关键是学会转化的思想,把问题转化为一元二次方程解决,学会利用公式恒等变形,属于中考常考题型.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
3.若关于x的方程x2-4x+k=0的一个根为2-$\sqrt{3}$,则k的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
13.如图,图(1)是一枚古代钱币,图(2)是类似图(1)的几何图形,将图(2)中的图形沿一条对称轴折叠得到图(3),关于图(3)描述正确的是( )


| A. | 只是轴对称图形 | |
| B. | 只是中心对称图形 | |
| C. | 既是轴对称图形又是中心对称图形 | |
| D. | 既不是轴对称图形也不是中心对称图形 |
 如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,则阴影部分的面积为4.
如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,则阴影部分的面积为4. 如图,A(3,0),C(0,2),矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,双曲线y=$\frac{k}{x}$经过点E,则k的值为( )
如图,A(3,0),C(0,2),矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,双曲线y=$\frac{k}{x}$经过点E,则k的值为( )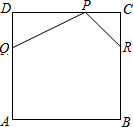 如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、
如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、