题目内容
2.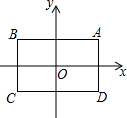 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
分析 首先求出点A′的坐标为(k,kt),再根据关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,可得mn=3,且n≠$\frac{3}{2}$;然后根据以m,n为坐标(记为(m,n))的所有的点中,有且只有一个点落在矩形A′B′C′D′的边上,可得反比例函数n=$\frac{3}{m}$的图象只经过点A′或C′;最后判断出反比例函数n=$\frac{3}{m}$的图象经过C′点,则
A′点的坐标是(2,$\frac{3}{2}$),所以k•t=,据此解答即可.
解答 解:∵矩形A′B′C′D′与矩形ABCD是位似图形,$\frac{A′B′}{AB}$=k,顶点A的坐标为(1,t),
∴点A′的坐标为(k,kt),
∵矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,
∴矩形A′B′C′D′也关于点O成中心对称.
∵关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,
∴mn=3,且n≠$\frac{3}{2}$,
即n=$\frac{3}{m}$(m≠2),
∵以m,n为坐标(记为(m,n)的所有的点中,有且只有一个点落在矩形A′B′C′D′的边上,
∴反比例函数n=$\frac{3}{m}$的图象只经过点A′或C′,
∵矩形A′B′C′D′关于点O成中心对称,反比例函数n=$\frac{3}{m}$的图象关于点O成中心对称,
∴反比例函数n=$\frac{3}{m}$的图象经过C′点,
如果反比例函数n=$\frac{3}{m}$的图象不经过C′点,
则以m,n为坐标(记为(m,n))的所有的点中,如果有点落在矩形A′B′C′D′的边上,
则至少有两个点落在矩形A′B′C′D′的边上,
∴A′点的坐标是(2,$\frac{3}{2}$),
∴k•t=$\frac{3}{2}$.
故选:D.
点评 (1)此题主要考查了位似变换问题,要熟练掌握,解答此题的关键是要明确:①两个图形必须是相似形;②对应点的连线都经过同一点;③对应边平行.
(2)此题还考查了二元一次方程组的求解方法,以及坐标与图形的性质,要熟练掌握.

| A. | $\left\{\begin{array}{l}{x+y=130}\\{3x+2y=60}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=130}\\{2x+3y=60}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=60}\\{3x+2y=130}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=60}\\{2x+3y=130}\end{array}\right.$ |
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 无法确定 |
| A. | 40° | B. | 140° | C. | 40°或140° | D. | 50° |