题目内容
4. 如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.
如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.(1)求A点和顶点C的坐标;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在直线OB下方的抛物线上是否存在点P,使得△POB的面积最大?若存在,求出△POB的最大面积;若不存在,请说明理由.
分析 (1)直接利用配方法以及一元二次方程的解法得出A,C点坐标;
(2)先确定A(3,0)和抛物线的对称轴,设B(x,x2-3x),再根据三角形面积公式得到$\frac{1}{2}$•3•|x2-3x|=6,则x2-3x=4或x2-3x=-4,然后分别解方程求出x即可确定满足条件的B点坐标;
(3)利用△POB的面积最大则此时P到OB的距离最大,即PO⊥OB时,进而得出P点坐标求出答案.
解答 解:(1)当y=0,则0=x2-3x,
故x(x-3)=0,
解得:x1=0,x2=3,
故A(3,0),
y=x2-3x=(x-$\frac{3}{2}$)2-$\frac{9}{4}$,
故C($\frac{3}{2}$,-$\frac{9}{4}$);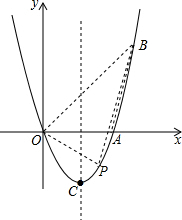
(2)设B(x,x2-3x),
因为△AOB的面积等于6,
所以$\frac{1}{2}$•3•|x2-3x|=6,
当x2-3x=4时,解得x1=-1,x2=4,则B点坐标为(4,4);
当x2-3x=-4时,方程无实数解.
所以点B的坐标为(4,4);
(3)∵在直线OB下方的抛物线上是否存在点P,使得△POB的面积最大,
∴此时P到OB的距离最大,即PO⊥OB时,
∵B(4,4),∴直线OB的解析式为:y=x,
∴OP的解析为:y=-x,则设P点坐标为:(x,-x),
∵P点在抛物线上,
∴y=x2-3x=-x,
解得:x1=0(不合题意舍去),x2=2,故P(2,-2),
∴OP=2$\sqrt{2}$,
∴△POB的面积最大为:$\frac{1}{2}$×OB×2$\sqrt{2}$=$\frac{1}{2}$×4$\sqrt{2}$×2$\sqrt{2}$=8.
点评 此题主要考查了二次函数综合以及三角形面积求法、配方法求抛物线顶点坐标等知识,正确得出P点位置是解题关键.

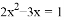 的二次项系数、一次项系数、常数项分别是()
的二次项系数、一次项系数、常数项分别是()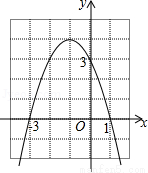
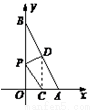
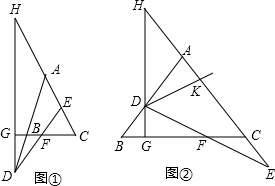 已知:如图,在△ABC中,AB=AC,点D,E分别是射线AB,射线AC上一动点,连接DE交BC于点F,且DF=EF,过点DG⊥CB交射线CB于点G,交CA的延长线于点H.
已知:如图,在△ABC中,AB=AC,点D,E分别是射线AB,射线AC上一动点,连接DE交BC于点F,且DF=EF,过点DG⊥CB交射线CB于点G,交CA的延长线于点H.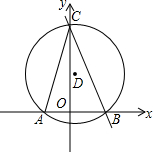 已知,如图,在平面直角坐标系中,A(-2,0),B(3,0),直线l:y=kx+b经过B点,与y轴的正半轴交于C点,连接AC.此时∠ACB=45°,有一⊙D经过△ABC的三个顶点.
已知,如图,在平面直角坐标系中,A(-2,0),B(3,0),直线l:y=kx+b经过B点,与y轴的正半轴交于C点,连接AC.此时∠ACB=45°,有一⊙D经过△ABC的三个顶点.