题目内容
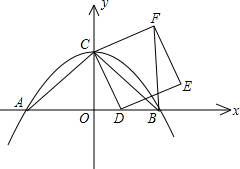 已知抛物线y=-
已知抛物线y=-| 1 |
| 4 |
(Ⅰ)求抛物线的解析式;
(Ⅱ)求证:BF⊥AB;
(Ⅲ)求∠FBE的度数;
(Ⅳ)当D点沿x轴正方向由点O移动以点B时,点E也随着运动,求出点E所走过的路线长是多少?直接写出结果,不必写过程.
考点:二次函数综合题
专题:
分析:(1)根据抛物线的对称性得到抛物线的对称轴为y轴,则b=0;然后利用方程与二次函数的关系求得点B、C的坐标,由S△OBC=8可以求得c的值;
(2)由抛物线y=-
x2+4交x轴于点A、B,当x=0,求出图象与y轴的交点坐标,以及y=0,求出图象与x轴的交点坐标,即可得出三角形的形状;首先证明△ACD≌△BCF,利用三角形的全等,得出∠ABF=∠ABC+∠CBF=90°,即可得出答案;
(3)如图,连接BE,过点E作EM⊥x轴于点M.易证△ODC≌△DME,则DM=OC=4,OD=EM.易求BM=EM.则∠MBE=∠MEB=45°;由(2)知,BF⊥AB,故
∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC的长度.
(2)由抛物线y=-
| 1 |
| 4 |
(3)如图,连接BE,过点E作EM⊥x轴于点M.易证△ODC≌△DME,则DM=OC=4,OD=EM.易求BM=EM.则∠MBE=∠MEB=45°;由(2)知,BF⊥AB,故
∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC的长度.
解答:解:(1)如图,∵AC=BC,
∴该抛物线的对称轴是y轴,则b=0.
∴C(0,c),B(
,0).
∵S△OBC=8,
∴
OC•OB=
×c×
=8,
解得c=4(c>0).
故该抛物线的解析式为y=-
x2+4;
(2)证明:由(1)得到抛物线的解析式为y=-
x2+4;
令y=0,得x1=4,x2=-4,
∴A(-4,0),B(4,0),
∴OA=OB=OC,
∴△ABC是等腰直角三角形;
如图,又∵四边形CDEF是正方形,
∴AC=BC,CD=CF,∠ACD=∠BCF,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(SAS),
∴∠CBF=∠CAD=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∴BF⊥AB;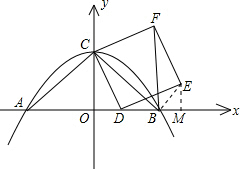
(3)如图,连接BE,过点E作EM⊥x轴于点M.
∵∠ODC+∠EDM=90°,∠EDM+∠DEM=90°,
∴∠CDO=∠DEM,
在△ODC和△MED中,
,
∴△ODC≌△DME(AAS),
∴DM=OC=4,OD=EM,
∵OD=OB-BD=4-BD=DM-BD=BM,
∴BM=EM.
∵∠EMB=90°,
∴∠MBE=∠MEB=45°;
由(2)知,BF⊥AB,
∴∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC=
=4
.
∴该抛物线的对称轴是y轴,则b=0.
∴C(0,c),B(
| 4c |
∵S△OBC=8,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 4c |
解得c=4(c>0).
故该抛物线的解析式为y=-
| 1 |
| 4 |
(2)证明:由(1)得到抛物线的解析式为y=-
| 1 |
| 4 |
令y=0,得x1=4,x2=-4,
∴A(-4,0),B(4,0),
∴OA=OB=OC,
∴△ABC是等腰直角三角形;
如图,又∵四边形CDEF是正方形,
∴AC=BC,CD=CF,∠ACD=∠BCF,
在△ACD和△BCF中,
|
∴△ACD≌△BCF(SAS),
∴∠CBF=∠CAD=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∴BF⊥AB;

(3)如图,连接BE,过点E作EM⊥x轴于点M.
∵∠ODC+∠EDM=90°,∠EDM+∠DEM=90°,
∴∠CDO=∠DEM,
在△ODC和△MED中,
|
∴△ODC≌△DME(AAS),
∴DM=OC=4,OD=EM,
∵OD=OB-BD=4-BD=DM-BD=BM,
∴BM=EM.
∵∠EMB=90°,
∴∠MBE=∠MEB=45°;
由(2)知,BF⊥AB,
∴∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC=
| 42+42 |
| 2 |
点评:本题考查了待定系数法求二次函数解析式、全等三角形的判定与性质、正方形和等腰直角三角形的性质,综合性强,考查学生数形结合的数学思想方法.(4)中弄清点E所走过的路程是解题的关键.

练习册系列答案
相关题目
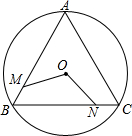 如图,M、N分别是⊙O的内接正△ABC的边AB、BC上的点且BM=CN,连接OM、ON,求∠MON的度数.
如图,M、N分别是⊙O的内接正△ABC的边AB、BC上的点且BM=CN,连接OM、ON,求∠MON的度数.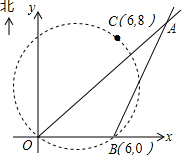 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.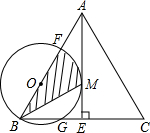 如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.
如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.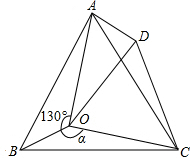 如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.