题目内容
(1)如图①,已知AB∥CD,求证:∠A+∠C=∠E
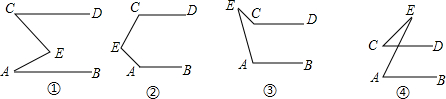
(2)直接写出当点E的位置分别如图②、图③、图④的情形时∠A、∠C、∠E之间的关系.
②中∠C、∠A、∠AEC之间的关系为
③中∠C、∠A、∠AEC之间的关系为
④中∠C、∠A、∠AEC之间的关系为
(3)在(2)中的3中情形中任选一种进行证明.

(2)直接写出当点E的位置分别如图②、图③、图④的情形时∠A、∠C、∠E之间的关系.
②中∠C、∠A、∠AEC之间的关系为
③中∠C、∠A、∠AEC之间的关系为
④中∠C、∠A、∠AEC之间的关系为
(3)在(2)中的3中情形中任选一种进行证明.
考点:平行线的性质
专题:
分析:(1)过E作EF∥AB的直线,根据内错角相等可得出三个角的关系;
(2)②过E作EF∥AB的直线,根据两直线平行,同旁内角互补可得出三个角的关系;③连接AC并延长,然后根据平行线的性质及外角的性质,可得出三个角的关系;④根据平行线的性质及外角的性质,可得出三个角的关系;
(3)在(2)中,选④进行证明,由平行线的性质可得:∠1=∠A,由外角的性质可得:∠1=∠C+∠AEC,然后将∠1=∠A,代换即可得证.
(2)②过E作EF∥AB的直线,根据两直线平行,同旁内角互补可得出三个角的关系;③连接AC并延长,然后根据平行线的性质及外角的性质,可得出三个角的关系;④根据平行线的性质及外角的性质,可得出三个角的关系;
(3)在(2)中,选④进行证明,由平行线的性质可得:∠1=∠A,由外角的性质可得:∠1=∠C+∠AEC,然后将∠1=∠A,代换即可得证.
解答:(1)证明:E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1=∠A,∠2=∠C,
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠C;
(2)②∠C+∠A+∠AEC=360°;
③∠C=∠A+∠AEC;
④∠A=∠AEC+∠C;
(3)在(2)中,选④进行证明,
∵AB∥CD,
∴∠1=∠A,
∵∠1=∠C+∠AEC,
∴∠A=∠C+∠AEC.

∵AB∥CD,
∴AB∥CD∥EF,
∴∠1=∠A,∠2=∠C,
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠C;
(2)②∠C+∠A+∠AEC=360°;
③∠C=∠A+∠AEC;
④∠A=∠AEC+∠C;
(3)在(2)中,选④进行证明,
∵AB∥CD,
∴∠1=∠A,
∵∠1=∠C+∠AEC,
∴∠A=∠C+∠AEC.

点评:此题考查了平行线的性质及三角形外角的性质,主要考查学生的推理能力和猜想能力.解题的关键是:灵活应用性质.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
6与-9的和为( )
| A、-3 | B、3 | C、15 | D、-15 |
下列条件,不能判定两个直角三角形全等的是( )
| A、斜边和一直角边对应相等 |
| B、两个锐角对应相等 |
| C、一锐角和斜边对应相等 |
| D、两条直角边对应相等 |
 如图所示,在Rt△ABC中,∠C=90°,∠B=40°,BC=10,解这个直角三角形(精确到0.1)(sin40°≈0.643,cos40°≈0.766,tan40°≈0.839)
如图所示,在Rt△ABC中,∠C=90°,∠B=40°,BC=10,解这个直角三角形(精确到0.1)(sin40°≈0.643,cos40°≈0.766,tan40°≈0.839) 如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,连AC.
如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,连AC. 世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)
世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上) 如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m到点C,测得仰角为60°,已知小敏同学身高(AB)为1.6m,求这棵树的高度(DF).(结果精确到0.1m,
如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m到点C,测得仰角为60°,已知小敏同学身高(AB)为1.6m,求这棵树的高度(DF).(结果精确到0.1m,