题目内容
3．
如图，小军、小英之间的距离为3m，他们在同一盏路灯下的影长均为1.8m，1.8m，已知小军、小英的身高分别为1.8m，1.5m，则路灯的高为3m．
分析 根据CD∥AB∥MN，得到△ABE∽△CDE，△ABF∽△MNF，根据相似三角形的性质可知$\frac{CD}{AB}$=$\frac{DE}{BE}$，$\frac{FN}{FB}$=$\frac{MN}{AB}$，即可得到结论．
解答 
解：如图，∵CD∥AB∥MN，
∴△ABE∽△CDE，△ABF∽△MNF，
∴$\frac{CD}{AB}$=$\frac{DE}{BE}$，$\frac{FN}{FB}$=$\frac{MN}{AB}$，即$\frac{1.8}{ab}$=$\frac{1.8}{1.8+BD}$，$\frac{1.5}{1.5+3-BD}$=$\frac{1.5}{AB}$
解得：AB=3m，
故答案为：3．
点评 本题考查的是相似三角形的应用，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA=1，OC=$\frac{1}{2}$，在第二象限内，以原点O为位似中心将矩形AOCB放大为原来的$\frac{3}{2}$倍，得到矩形A1OC1B1，再以原点O为位似中心将矩形
如图，在△ABC中，AC=3cm，∠ACB=90°，∠ABC=60°，将△ABC绕点B顺时针旋转至△A′BC′，点C′在直线AB上，则边AC扫过区域（图中阴影部分）的面积为3π cm2．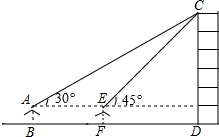
某数学兴趣小组在学习了《锐角三角函数》以后，开展测量物体高度的实践活动，测量一建筑物CD的高度，他们站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走20m，到达点F处测得楼顶C的仰角为45°（BFD在同一直线上）．已知观测员的眼睛与地面距离为1.5m（即AB=1.5m），求这栋建筑物CD的高度．（参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414．结果保留整数）
如图，△ABC中，CA=CB，AB=6，CD=4，E是高线CD的中点，以CE为半径作⊙C，G是⊙C上一个动点，P是AG中点，则DP的最大值为$\frac{7}{2}$．
6．菲尔兹奖是国际上有崇高声誉的一个数学奖项，下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄（岁）：
29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
请根据上述数据，解答下列问题：
小彬按“组距为5”列出了如图的频数分布表
（1）每组数据含最小值不含最大值，请将表中空缺的部分补充完整，并补全频数分布直方图；
（2）根据（1）中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征；
（3）在（1）的基础上，小彬又画了如图所示的扇形统计图，图中获奖年龄在30～35岁的人数约占获奖总人数的26.8%（百分号前保留1位小数）；C组所在扇形对应的圆心角度数约为199°（保留整数）
29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
请根据上述数据，解答下列问题：小彬按“组距为5”列出了如图的频数分布表
| 分组 | 频数 |
| A：25～30 | 4 |
| B：30～35 | 15 |
| C：35～40 | 31 |
| D：40～45 | 6 |
| 合计 | 56 |
（2）根据（1）中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征；
（3）在（1）的基础上，小彬又画了如图所示的扇形统计图，图中获奖年龄在30～35岁的人数约占获奖总人数的26.8%（百分号前保留1位小数）；C组所在扇形对应的圆心角度数约为199°（保留整数）