题目内容
2.给出下列算式:32-12=8=8×1;
52-32=16=8×2;
72-52=24=8×3;
92-72=32=8×4.
(1)观察上面一系列式子,你能发现什么规律?用含n的式子表示出来(n为正整数).
(2)试利用第(1)题一系列反应规律的算式,能求出1+2+3+…+n(n为正整数)的公式.
分析 (1)两个连续奇数的平方差等于8的倍数,由此得出第n个等式为(2n+1)2-(2n-1)2=8n,由此解决问题即可;
(2)利用(1)中的规律求得答案即可.
解答 解:(1)∵32-12=8=8×1;
52-32=16=8×2:
72-52=24=8×3;
92-72=32=8×4
…
∴第n个等式为(2n+1)2-(2n-1)2=8n;
(2)把(1)中的两边的式子相加得
8×(1+2+3+4+…+n)=(2n+1)2-12
1+2+3+4+…+n=$\frac{2n(2n+2)}{8}$=$\frac{n(n+1)}{2}$.
点评 此题考查数字的变化规律,根据数字的特点,得出运算的规律,利用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列说法中,正确的是( )
| A. | 角的两边画的越长,这个角就越大 | |
| B. | 角的大小与角的两边所画的长短无关 | |
| C. | 角的大小和它们的度数的大小是不一致的 | |
| D. | 角大,它的度数不一定大 |
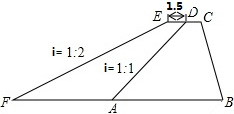 如图,为了防洪,某地区计划将长为1000m的一堤面加宽1.5m,背水坡坡度由原来1:1改为1:2,已知原背水坡坡长AD=8.0m,求完成这一工程所需的土方.(精确到1m3,$\sqrt{2}$≈1.414)
如图,为了防洪,某地区计划将长为1000m的一堤面加宽1.5m,背水坡坡度由原来1:1改为1:2,已知原背水坡坡长AD=8.0m,求完成这一工程所需的土方.(精确到1m3,$\sqrt{2}$≈1.414)