题目内容
19.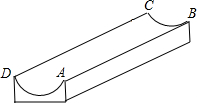 如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)
如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)
分析 要求滑行的最短距离,需将该U型池的侧面展开,进而根据“两点之间线段最短”得出结果.
解答 解:其侧面展开图如图:作点C关于AB的对称点F,连接DF,
∵中间可供滑行的部分的截面是半径为5m的半圆,
∴BC=πR=5π=15m,AB=CD=20m,
∴CF=30m,
在Rt△CDF中,DF=$\sqrt{C{F}^{2}+C{D}^{2}}=\sqrt{3{0}^{2}+2{0}^{2}}=10\sqrt{13}$m,
故他滑行的最短距离约为10$\sqrt{13}$m.
故答案为:10$\sqrt{13}$.
点评 本题考查的是平面展开-最短路径问题,此题就是把U型池的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
9.一元二次方程x2-9x+18=0的两根是一等腰三角形的底和腰,则这个等腰三角形的周长为( )
| A. | 12 | B. | 12或15 | C. | 15 | D. | 无法确定 |
4.下列整式能直接利用完全平方公式分解因式的是( )
| A. | x2-4 | B. | x2+6x+9 | C. | x2-2x-1 | D. | x2+y2 |
11.以下列各组线段长为边,能组成三角形的是( )
| A. | 1cm,2cm,4cm | B. | 7cm,6cm,5cm | C. | 12cm,6cm,6cm | D. | 2cm,3cm,6cm |
 如图,等边△ABC的边长为6,D为BC上一点,且BD=2,E为AC上一点,若∠ADE=60°,则CE的长为$\frac{4}{3}$.
如图,等边△ABC的边长为6,D为BC上一点,且BD=2,E为AC上一点,若∠ADE=60°,则CE的长为$\frac{4}{3}$.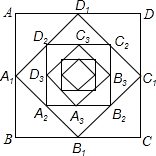 如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是$\frac{1}{2}$.
如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是$\frac{1}{2}$.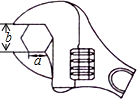 如图,要拧开一个正六边形螺帽,已知扳手张开的开口b长为2cm,螺帽的边长为a为$\frac{2\sqrt{3}}{3}$cm.
如图,要拧开一个正六边形螺帽,已知扳手张开的开口b长为2cm,螺帽的边长为a为$\frac{2\sqrt{3}}{3}$cm.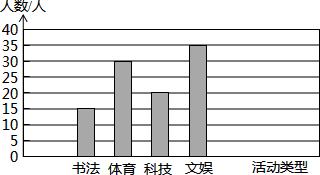 某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示.根据图示所提供的样本数据,可得学生参加体育活动的频率是0.3.
某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示.根据图示所提供的样本数据,可得学生参加体育活动的频率是0.3.