题目内容
7.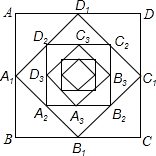 如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是$\frac{1}{2}$.
如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是$\frac{1}{2}$.
分析 根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点的正方形A1B1C1D1的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形A8B8C8D8的周长.
解答 解:顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则得正方形A1B1C1D1的面积为正方形ABCD面积的一半,即$\frac{1}{2}$,则周长是正方形ABCD的$\frac{\sqrt{2}}{2}$;
顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2,则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半,即正方形ABCD的$\frac{1}{4}$,则周长是正方形ABCD的$\frac{1}{2}$;
顺次连接正方形A2B2C2D2得正方形A3B3C3D3,则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半,即正方形ABCD的$\frac{1}{8}$,则周长是正方形ABCD的$\frac{\sqrt{2}}{4}$;
顺次连接正方形A3B3C3D3中点得正方形A4B4C4D4,则正方形A4B4C4D4的面积为正方形A3B3C3D3面积的一半,即正方形ABCD的$\frac{1}{16}$,则周长是正方形ABCD的$\frac{1}{4}$;
…
故第n个正方形周长是原来的$\sqrt{\frac{1}{{2}^{n}}}$,
以此类推:正方形A8B8C8D8周长是原来的$\frac{1}{16}$,
∵正方形ABCD的边长为2,周长为8,
∴按此方法得到的四边形A8B8C8D8的周长为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了利用了三角形的中位线的性质,相似图形的面积比等于相似比的平方的性质.进而得到周长关系.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (2ab+1)厘米 | B. | 8a2b厘米 | C. | (4ab+2)厘米 | D. | (4a2b-2a)厘米 |
| A. | 0 | B. | 4 | C. | 0或2 | D. | 4或0 |
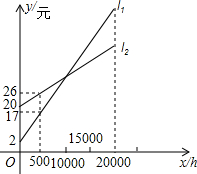 如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,
如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象, 如图所示,一根旗杆被风刮倒,从离地面8米的A处断裂,旗杆顶落在地面距离底部C点15米的B处,则旗杆在断裂之前有多高?
如图所示,一根旗杆被风刮倒,从离地面8米的A处断裂,旗杆顶落在地面距离底部C点15米的B处,则旗杆在断裂之前有多高?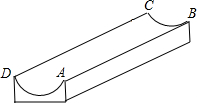 如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)
如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)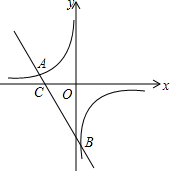 如图所示,直线y=-2x+b与反比例函数$y=\frac{k}{x}$交于点A、B,与x轴交于点C.
如图所示,直线y=-2x+b与反比例函数$y=\frac{k}{x}$交于点A、B,与x轴交于点C.