题目内容
10. 如图,等边△ABC的边长为6,D为BC上一点,且BD=2,E为AC上一点,若∠ADE=60°,则CE的长为$\frac{4}{3}$.
如图,等边△ABC的边长为6,D为BC上一点,且BD=2,E为AC上一点,若∠ADE=60°,则CE的长为$\frac{4}{3}$.
分析 根据相似三角形的判定定理求出△ABD∽△DCE,再根据相似三角形对应边的比等于相似比的平方解答.
解答 解:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠ADB=∠DAC+∠C,∠DEC=∠DAC+∠ADE,
∵∠ADE=60°,
∴∠ADB=∠DAC+60°,∠DEC=∠DAC+60°,
∴∠ADB=∠DEC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE,
∴$\frac{AB}{DC}$=$\frac{BD}{CE}$,
∴$\frac{6}{4}$=$\frac{2}{CE}$,
∴CE=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 本题考查了相似三角形的性质和判定,找准相似三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
 如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
18.一张长为4a厘米矩形纸片的面积为(8a2b+4a)平方厘米,则此矩形的宽为( )
| A. | (2ab+1)厘米 | B. | 8a2b厘米 | C. | (4ab+2)厘米 | D. | (4a2b-2a)厘米 |
 如图,在△ABC中,P为AB上一点,则下列四个条件中
如图,在△ABC中,P为AB上一点,则下列四个条件中 如图所示,一根旗杆被风刮倒,从离地面8米的A处断裂,旗杆顶落在地面距离底部C点15米的B处,则旗杆在断裂之前有多高?
如图所示,一根旗杆被风刮倒,从离地面8米的A处断裂,旗杆顶落在地面距离底部C点15米的B处,则旗杆在断裂之前有多高?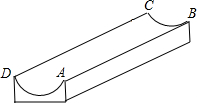 如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)
如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20m,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为10$\sqrt{13}$m.(π取3)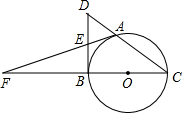 如图 A是以BC为直径的⊙O上一点,过点B作⊙O的切线,与CA的延长线交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.求证:AF是⊙O的切线.
如图 A是以BC为直径的⊙O上一点,过点B作⊙O的切线,与CA的延长线交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.求证:AF是⊙O的切线.