题目内容
9.要使代数式$\frac{{\sqrt{1-x}}}{x+2}$有意义,则x的取值范围是( )| A. | x≥1 | B. | x≤1 | C. | x≥1且x≠-2 | D. | x≤1且x≠-2 |
分析 根据二次根式有意义的条件可得1-x≥0,根据分式有意义的条件可得x+2≠0,再解即可.
解答 解:由题意得:1-x≥0,且x+2≠0,
解得:x≤1,且x≠-2,
故选:D.
点评 此题主要考查了二次根式和分式有意义的条件,关键是掌握二次根式中的被开方数必须是非负数,分式有意义的条件是分母不等于零.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.对于任意两个实数对(a,b),和(c,d),当且仅当a=c且b=d时,(a,b)=(c,d).我们现在定义新运算“※”:(a,b)※(c,d)=(a2-c,b+d2).若(2,x)※(y,5)=(3,34),则xy的值为( )
| A. | 3 | B. | -3 | C. | 9 | D. | -9 |
17.$\sqrt{8n}$是整数,正整数n的最小值是( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
19.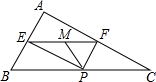 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )| A. | 1.2 | B. | 1.3 | C. | 1.4 | D. | 2.4 |
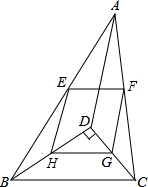 如图,点D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,点E,F,G,H分别是线段AB,AC,CD,BD的中点.
如图,点D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,点E,F,G,H分别是线段AB,AC,CD,BD的中点.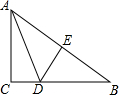 如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )
如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )