题目内容
4.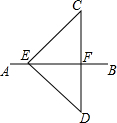 如图,已知AB是线段CD的垂直平分线,E是AB上一点,如果EC=10,EF=8,那么DF=6.
如图,已知AB是线段CD的垂直平分线,E是AB上一点,如果EC=10,EF=8,那么DF=6.
分析 根据勾股定理求出CF,根据线段垂直平分线的性质得到DF=CF,得到答案.
解答 解:∵CD⊥AB,EC=10,EF=8,
∴CF=$\sqrt{C{E}^{2}-E{F}^{2}}$=6,
∵AB是线段CD的垂直平分线,
∴DF=CF=6,
故答案为:6.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列命题中,属于假命题的是( )
| A. | 如果a>b,那么-a<-b | |
| B. | 等角的余角相等 | |
| C. | 等式的两边同加上或同减去一个式子,结果仍为等式 | |
| D. | 如果a+b>0,那么a>0,b>0 |
19.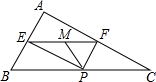 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )| A. | 1.2 | B. | 1.3 | C. | 1.4 | D. | 2.4 |
9.已知等腰三角形的周长为20cm,底边长为y(cm),腰长为x(cm),y与x的函数关系式为y=20-2x,那么自变量x的取值范围是( )
| A. | x>0 | B. | 0<x<10 | C. | 0<x<5 | D. | 5<x<10 |
16.掷一枚均匀的骰子(正方体),骰子的每个面上分别标有数字1、2、3、4、5、6,则3的倍数朝上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
13. 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )
 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )| A. | ∠1、∠3是同位角 | B. | ∠1、∠2是同旁内角 | C. | ∠1、∠5是同位角 | D. | ∠5、∠6是内错角 |
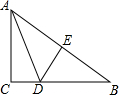 如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )
如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )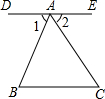 完成下列推理过程.
完成下列推理过程.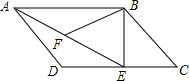 如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.