题目内容
9.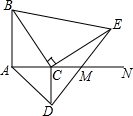 如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为4.
如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为4.
分析 如图作EH⊥AN于H,由△ABC≌△HCE得AB=CH,AC=EH,再证明△DCM≌△EHM得CM=HM即可解决问题.
解答 解:如图作EH⊥AN于H,
∵BA⊥AN,EH⊥AN,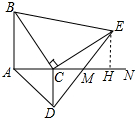
∴∠BAC=∠EHC=90°,
∵∠ABC+∠ACB=90°,∠ACB+∠ECH=90°,
∴∠ABC=∠ECH,
∵△BCE和△ACD都是等腰三角形,
∴BC=CE,AC=DC,∠BCE=∠ACD=90°
在△ABC和△HCE中,
$\left\{\begin{array}{l}{∠BAC=∠EHC}\\{∠ABC=∠HCE}\\{BC=CE}\end{array}\right.$
∴△ABC≌△HCE,
∴AC=EH=CD,AB=CH,
在△DCM和△EHM中,
$\left\{\begin{array}{l}{CD=EH}\\{∠DCM=∠EHM}\\{∠CMD=∠EMH}\end{array}\right.$,
∴△DCM≌△EHM.
∴CM=HM,
∴CM=$\frac{1}{2}$CH=$\frac{1}{2}$AB=4.
故答案为4.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质,解题的关键是添加辅助线构造全等三角形,掌握添加辅助线的方法,属于中考常考题型.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
19.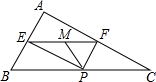 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )| A. | 1.2 | B. | 1.3 | C. | 1.4 | D. | 2.4 |
20.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
| A. | 等于4cm | B. | 大于4cm而小于5cm | ||
| C. | 不大于4cm | D. | 小于4cm |
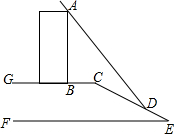 如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)
如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)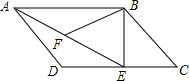 如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.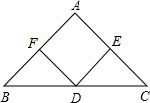 如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,使四边形AFDE为菱形,应添加的条件是AF=AE(添加一个条件即可).
如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,使四边形AFDE为菱形,应添加的条件是AF=AE(添加一个条件即可).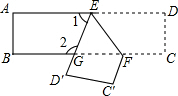 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在D′、C′的位置上.如图所示,若∠EFG=60°,求∠1与∠2的度数.
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在D′、C′的位置上.如图所示,若∠EFG=60°,求∠1与∠2的度数.