题目内容
20．矩形两条对角线的夹角为60°，其中矩形中较短的边长为5，则矩形对角线的长为10．分析 首先根据题意画出图形，然后由矩形两条对角线的夹角为60°，证得△AOB是等边三角形，继而求得答案．
解答 
解：如图，∵四边形ABCD是矩形，
∴OA=$\frac{1}{2}$AC，OB=$\frac{1}{2}$BD，AC=BD，
∴OA=OB，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=5，
∴AC=2OA=10．
即矩形对角线的长为10．
故答案为：10．
点评 此题考查了矩形的性质以及等边三角形的判定与性质．注意根据题意画出图形，结合图形求解是关键．
练习册系列答案
相关题目
6．sin30°=（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
如图所示，OC为∠AOB的角平分线，
如图，图中所有的三角形都是直角三角形，四边形都是正方形，其中最大正方形E的边长为10，则四个正方形A，B，C，D的面积之和为100．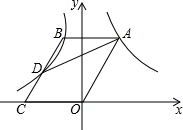
如图，点A在双曲线y=$\frac{6}{x}$（x＞0）上，点B在双曲线y=-$\frac{3}{x}$（x＜0）上，且AB平行于x轴，BC∥AO交x轴于点C，交双曲线y=-$\frac{3}{x}$（x＜0）于点D，连接AD．