题目内容
15.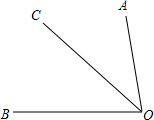 如图所示,OC为∠AOB的角平分线,
如图所示,OC为∠AOB的角平分线,(1)作图:
①在OA边上任取一点P,过点P作PD∥OB,交OC于点D;
②过点D作DE⊥OB,垂足为点E.
(2)求∠PDE的度数.
(3)若∠PDO=40°,求∠AOB的度数.
分析 (1)利用题中几何语言画图;
(2)先根据垂直的定义得到∠DEO=90°,然后根据平行线的性质计算∠PDE的度数;
(3)先根据平行线的性质得到∠PDO=∠DOE=40°,然后根据角平分线的定义计算∠AOB的度数.
解答 解:(1)如图,
(2)∵DE⊥OB,
∴∠DEO=90°,
∵PD∥OB,
∴∠PDE+∠DEO=180°,
∴∠PDE=180°-∠DEO=180°-90°=90°;
(3)∵PD∥OB,
∴∠PDO=∠DOE,
∵∠PDO=40°,
∴∠DOE=40°,
∵OC平分∠AOB,
∴∠AOB=2∠DOE=80°.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行线的性质.

练习册系列答案
相关题目
6.下列根据等式的性质变形正确的是( )
| A. | 由3x-2=2x+2,得x=4 | B. | 由-$\frac{1}{3}x=\frac{2}{3}$,得x=2 | ||
| C. | 由2x-3=3x,得x=3 | D. | 由3x-5=7,得3x=7-5 |
4. 如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(1,-3),则当x>1时,y1与y2的大小关系为( )
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(1,-3),则当x>1时,y1与y2的大小关系为( )
 如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(1,-3),则当x>1时,y1与y2的大小关系为( )
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(1,-3),则当x>1时,y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
5.下列命题中,真命题的是( )
| A. | 如果一个四边形两条对角线相等,那么这个四边形是矩形 | |
| B. | 如果一个四边形两条对角线相互垂直,那么这个四边形是菱形 | |
| C. | 如果一个平行四边形两条对角线平分所在的角,那么这个平行四边形是菱形 | |
| D. | 如果一个四边形两条对角线相互垂直平分,那么这个四边形是矩形 |
 如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.
如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.