题目内容
19.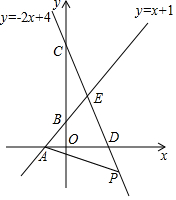 如图,直线y=x+1与x,y轴交于点A,B,直线y=-2x+4与x、y轴交于点D,C,这两条直线交于点E.
如图,直线y=x+1与x,y轴交于点A,B,直线y=-2x+4与x、y轴交于点D,C,这两条直线交于点E.(1)求E点坐标;
(2)若P为直线CD上一点,当△ADP的面积为9时,求P的坐标.
分析 (1)将y=x+1与y=-2x+4联立,求得方程组的解即可;
(2)先求得点A和点D的坐标,从而可得到AD的长,然后利用三角形的面积公式可求得点P的纵坐标的绝对值,然后将点P的纵坐标代入函数解析式求得对应的x的值即可.
解答 解:(1)将y=x+1代入y=-2x+4得:x+1=-2x+4,解得:x=1,
将x=1代入y=x+1得:y=2.
∴点E的坐标为(1,2).
(2)把y=0代入y=x+1得:x+1=0,解得x=-1,
∴A(-1,0).
把y=0代入y=-2x+4得:-2x+4=0,解得x=2,
∴A(2,0).
∴AD=3.
∵△ADP的面积为9,
∴$\frac{1}{2}$×3×|yP|=9,解得:|yP|=6.
∴yP=6或yP=-6.
将y=6代入y=-2x+4得:-2x+4=6,解得:x=-1,
∴P(-1,6).
将y=-6代入y=-2x+4得:-2x+4=-6,解得:x=5,
∴P(5,-6).
综上所述,点P的坐标为(-1,6)或(5,-6).
点评 本题主要考查的是一次函数的综合应用,依据三角形的面积公式求得点P的纵坐标是解题的关键.

练习册系列答案
相关题目
14.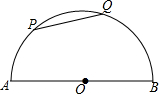 如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则$\widehat{AP}$与$\widehat{QB}$的长度之和为( )
如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则$\widehat{AP}$与$\widehat{QB}$的长度之和为( )
 如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则$\widehat{AP}$与$\widehat{QB}$的长度之和为( )
如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则$\widehat{AP}$与$\widehat{QB}$的长度之和为( )| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | π |
11.在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如表所示:
(1)求这次调查的50名学生读书的册数的平均数和众数.
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
8.某校要从小明和小芳两名同学中挑选一人参加全县环保知识竞赛,在最近的五次选拔测试中,两人的成绩如下表:
根据上表解答下列问题:
(1)分别计算两人成绩的平均数和方差;
(2)学校会派哪个同学去参加全县比赛?为什么?
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 小明 | 60 | 75 | 100 | 90 | 75 |
| 小芳 | 70 | 80 | 90 | 80 | 80 |
(1)分别计算两人成绩的平均数和方差;
(2)学校会派哪个同学去参加全县比赛?为什么?
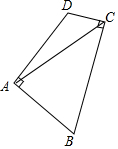 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为18.
如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为18.