题目内容
19.已知$\frac{5{x}^{2}-8x+2}{{x}^{3}-2{x}^{2}-2x+1}$=$\frac{A}{x+1}$+$\frac{Bx+C}{{x}^{2}-3x+1}$,求A,B,C.分析 已知等式整理后,利用分式相等的条件求出A,B,C的值即可.
解答 解:已知等式整理得:$\frac{5{x}^{2}-8x+2}{(x+1)({x}^{2}-3x+1)}$=$\frac{A({x}^{2}-3x+1)+(x+1)(Bx+C)}{(x+1)({x}^{2}-3x+1)}$,
∴5x2-8x+2=(A+B)x2+(B+C-3A)x+A+C,
∴$\left\{\begin{array}{l}{A+B=5}\\{B+C-3A=-8}\\{A+C=2}\end{array}\right.$,
解得:A=3,B=2,C=-1.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.两个锐角分别相等的两个直角三角形( )全等.
| A. | 不一定 | B. | 一定不 | C. | 一定 | D. | 以上都不对 |
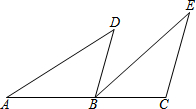 已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB.
已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB. 设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号.
设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号. 已知函数y=-x2+bx+2b-1的部分图象如图所示,求函数的解析式.
已知函数y=-x2+bx+2b-1的部分图象如图所示,求函数的解析式. 如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$.
如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$. △ABC中,l垂直平分AB交AC于P,交AB于Q,△ABC周长为26cm,AQ=4cm,求△PCB的周长.
△ABC中,l垂直平分AB交AC于P,交AB于Q,△ABC周长为26cm,AQ=4cm,求△PCB的周长.