题目内容
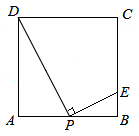
如图,在边长10cm为的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为 cm。
 .
.
【解析】
试题分析:设AP=x,BE=y.通过△ABP∽△PCQ的对应边成比例得到 ,所以
,所以 ,即y=-
,即y=- x2+x.利用“配方法”求该函数的最大值.
x2+x.利用“配方法”求该函数的最大值.
试题解析:设AP=x,BE=y.
如图,

∵四边形ABCD是正方形,
∴∠A=∠B=90°
∵PE⊥DP,
∴∠2+∠3=90°,∠1+∠2=90°
∴∠1=∠3,
∴△ADP∽△BPE,
∴ ,即
,即 ,
,
∴y=- x2+x=-
x2+x=- (x-5)2+
(x-5)2+ (0<x<10);
(0<x<10);
∴当x=5时,y有最大值 .
.
考点:1.相似三角形的判定与性质;2.二次函数的最值;3.正方形的性质.

练习册系列答案
相关题目

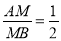 ,则
,则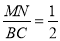 ;
;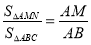 ;
;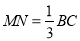 ,则
,则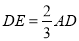 .
.
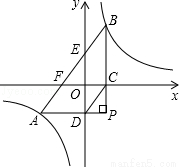
 时,求点P的坐标.
时,求点P的坐标.
 ,求⊙O的直径.
,求⊙O的直径.
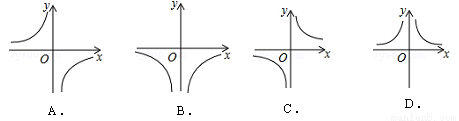
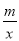 的大致图象是( )
的大致图象是( )