题目内容
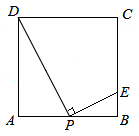
(本小题满分10分)已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为点E,点F在BD上,连接AF,EF.

(1)求证:AD=ED;
(2)如果AF∥CD,求证:四边形ADEF是菱形.
见解析
【解析】
试题分析:(1)根据条件证明ΔABD≌ΔEBD,可得AD=ED;(2)由(1)知AD=ED,所以要证明四边形ADEF是菱形,只需要证明AF∥DE,AF=DE,得四边形ADEF是平行四边形即可.
试题解析:证明:(1)∵BC=CD,∴∠CDB=∠CBD.
∵AD∥BC,∴∠ADB=∠CBD.∴∠ADB=∠CDB.(2分)
又∵AB⊥AD,BE⊥CD,∴∠BAD=∠BED=90°.
于是,在ΔABD和ΔEBD中,∵∠ADB=∠CDB,
∠BAD=∠BED,BD=BD,∴ΔABD≌ΔEBD. (4分)
∴AD=ED. (5分)
(2) ∵AF∥CD,∴∠AFD=∠EDF.
∴∠AFD=∠ADF,即得AF=AD. (7分)
又∵AD=ED,∴AF=DE.
于是,由AF∥DE,AF=DE,
得四边形ADEF是平行四边形. (9分)
又∵AD=ED,∴四边形ADEF是菱形. (10分)
考点:1. 等腰三角形的性质2. 全等三角形的判定与性质;3. 菱形的判定.

练习册系列答案
相关题目
 ,则
,则 ( )
( ) B、
B、 C、
C、 D、
D、
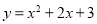 绕着它与
绕着它与 轴的交点旋转180°,所得抛物线的解析式是( ).
轴的交点旋转180°,所得抛物线的解析式是( ).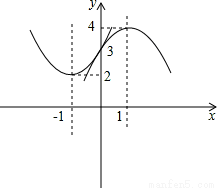
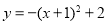 B.
B.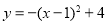
 D.
D.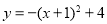
 的整数解共有( )
的整数解共有( ) 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.