题目内容
如图,AB是⊙O的直径,弦CD⊥AB于点N,点M在⊙O上,∠1=∠C
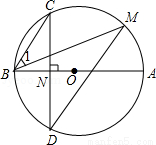
(1)求证:CB∥MD;
(2)若BC=4,sinM= ,求⊙O的直径.
,求⊙O的直径.
(1)证明见解析;(2)6.
【解析】
试题分析:(1)由∠C与∠M是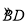 所对的圆周角,根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠C=∠M,又由∠1=∠C,易得∠1=∠M,即可判定CB∥MD;
所对的圆周角,根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠C=∠M,又由∠1=∠C,易得∠1=∠M,即可判定CB∥MD;
(2)首先连接AC,AB为⊙O的直径,可得∠ACB=90°,又由弦CD⊥AB,根据垂径定理的即可求得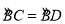 ,继而可得∠A=∠M,又由BC=4,sinM=
,继而可得∠A=∠M,又由BC=4,sinM=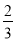 ,即可求得⊙O的直径.
,即可求得⊙O的直径.
试题解析:(1)证明:∵∠C与∠M是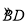 所对的圆周角,
所对的圆周角,
∴∠BCD=∠M,
又∵∠1=∠C,
∴∠1=∠M,
∴CB∥MD;
(2)【解析】
连接AC,

∵AB为⊙O的直径,
∴∠ACB=90°,
又∵CD⊥AB,
∴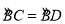
∴∠A=∠M,
∴sinA=sinM,
在Rt△ACB中,sinA=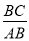 ,
,
∵sinM=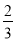 ,BC=4,
,BC=4,
∴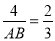
解得,AB=6,
即⊙O的直径为6.
考点:1.圆周角定理;2.垂径定理;3解直角三角形.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
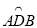 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
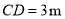 ,标杆与旗杆
,标杆与旗杆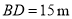 ,人的眼睛与地面的高度
,人的眼睛与地面的高度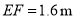 ,人与标杆
,人与标杆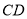 的水平距离
的水平距离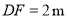 ,人的
,人的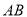 的高度.
的高度. 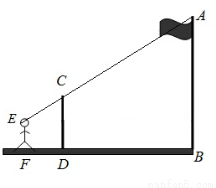

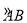 所在⊙O的半径为2,AB=2
所在⊙O的半径为2,AB=2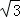 .点P为优弧
.点P为优弧
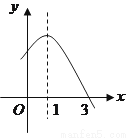
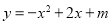 的部分图象如右图所示,则关于
的部分图象如右图所示,则关于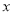 的一元二次方程
的一元二次方程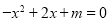 的解为__________。
的解为__________。