题目内容
16.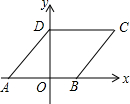 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A、B的坐标分别为(-3,0)、(2,0),且点D在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为20.
如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A、B的坐标分别为(-3,0)、(2,0),且点D在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为20.
分析 直接利用菱形的性质得出各边长,进而利用勾股定理得出DO的长,即可得出C点坐标,再利用反比例函数的性质得出k的值.
解答 解:由题意可得:AB=DC=AD=BC=5,
故DO=$\sqrt{{5}^{2}-{3}^{2}}$=4,
则C(5,4),
故k=xy=4×5=20.
故答案为:20.
点评 此题主要考查了菱形的性质以及勾股定理和反比例函数图形上点的坐标特点,得出C点坐标是解题关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
6.下列方程是一元一次方程的是( )
| A. | x2-x=2 | B. | x+5y=3 | C. | $\frac{1}{x}$+1=$\frac{x}{2}$ | D. | $\frac{1}{2}$+x=$\frac{x}{5}$ |
4.将下列多项式分解因式,结果中不含因式x+1的是( )
| A. | x2-1 | B. | x2-2x+1 | C. | x(x-2)+(x-2) | D. | x2+2x+1 |
11.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 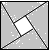 | B. |  | C. | 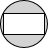 | D. | 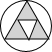 |
5. 老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )
老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )
 老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )
老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
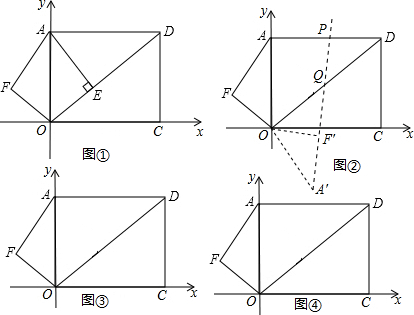
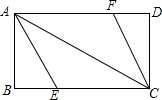 同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).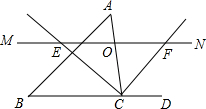 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.