题目内容
1．
如图，AB是⊙O的直径，点C是圆上一点，∠BAC=70°，则∠OCB的度数为（ ）| A． | 10° | B． | 20° | C． | 30° | D． | 40° |
分析 先根据圆周角定理求出∠BOC的度数，再由等腰三角形的性质即可得出结论．
解答 解：∵∠BAC=70°，
∴∠BOC=2∠BAC=140°，
∴∠OCB=$\frac{180°-140°}{2}$=20°．
故答案为：20°．
故选B．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
11．
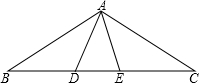如图，∠ADB=∠AEC=100°，∠BAD=50°，BD=EC，则∠C=（ ）
如图，∠ADB=∠AEC=100°，∠BAD=50°，BD=EC，则∠C=（ ）| A． | 20° | B． | 50° | C． | 30° | D． | 40° |
16．在一个布袋里装有白球6只、红球2只、黑球4只，它们除颜色外没有任何区别，从袋中随机取出1只球，则取出红球的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |
6．正六边形的两条对边之间的距离是2$\sqrt{3}$，则它的边长是（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
13．下列运算正确的是（ ）
| A． | a2•a3=a6 | B． | （a2）3=a5 | C． | （-2a2b）3=-8a6b3 | D． | （a-b）2=a2-b2 |
一个几何体由几个大小相同的小立方块搭成，从上面和从左面看到的这个几何体的形状如图所示，则从正面看搭的这个几何体，有（ ）种不同形状的图形．
11．下列说法错误的是（ ）
| A． | 三角形的内切圆与三角形的三边都相切 | |
| B． | 一个三角形一定有唯一一个内切圆 | |
| C． | 一个圆一定有唯一一个外切三角形 | |
| D． | 等边三角形的内切圆与外接圆是同心圆 |