题目内容
17.有理数a,b在数轴上的位置如图所示,则在下列结论中正确的个数有( )①ab<0②a+b>0③a2>b2④a<-b<b<-a
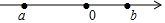
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据图示,可得a<0<b,-a>b,据此逐项判断即可.
解答 解:∵a<0<b,
∴ab<0,
∴选项①正确;
∵a<0<b,-a>b,
∴a+b<0,
∴选项②不正确;
∵a<0<b,-a>b,
∴a2>b2,
∴选项③正确;
∵a<0<b,-a>b,
∴a<-b<b<-a,
∴选项④正确,
∴正确的结论有3个:①、③、④.
故选:C.
点评 此题主要考查了有理数大小比较的方法,以及数轴的特征和应用,要熟练掌握.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
7.甲队有工人96人,乙队有工人72人,如果要求乙队的人数是甲队人数的$\frac{1}{3}$,应从乙队调 多少人去甲队?如果设应从乙队调x人到甲队,列出的方程正确的是( )
| A. | 96+x=$\frac{1}{3}$(72-x) | B. | $\frac{1}{3}$(96+x)=72-x | C. | $\frac{1}{3}$(96-x)=72-x | D. | $\frac{1}{3}$×96+x=72-x |
8.运用等式的性质变形正确的是( )
| A. | 如果a=b,那么a+c=b-c | B. | 如果a=3,那么a2=3a2 | ||
| C. | 如果a=b,那么$\frac{a}{c}$=$\frac{b}{c}$ | D. | 如果$\frac{a}{c}$=$\frac{b}{c}$,那么a=b |
5. 如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
 如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
2. 如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
 如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{17}$ |
6.正六边形的两条对边之间的距离是2$\sqrt{3}$,则它的边长是( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
7.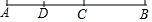 如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为( )
如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为( )
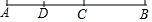 如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为( )
如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为( )| A. | 2cm | B. | 4cm | C. | 8cm | D. | 13cm |



