题目内容
18.如果一个正九边形的半径是R,那么它的边长是2Rsin20°.分析 根据题意画出图形,由正九边形的性质求出∠AOB的度数,作OD⊥AB,由垂径定理可知AD=BD=$\frac{1}{2}$AB,∠AOD=$\frac{1}{2}$∠AOB,再利用锐角三角函数的定义求出AB的长即可.
解答 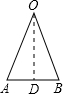 解:如图所示,
解:如图所示,
过O作OD⊥AB于点D,则AD=BD=$\frac{1}{2}$AB,
∵此多边形是正九边形,
∴∠AOB=$\frac{360°}{9}$=40°,
∴∠AOD=20°,
在Rt△AOD中,AD=OAsin∠AOD=Rsin20°,
∴AB=2AD=2Rsin20°;
故答案为:2Rsin20°.
点评 本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
7.下列说法,正确的是( )
| A. | 相等的两个角是对顶角 | |
| B. | 邻补角是互补的两个角,互补的两个角也是邻补角 | |
| C. | 如果两个角有公共顶点和一条公共边,那么它们互为邻补角 | |
| D. | 两条直线相交,如果它们所成的邻补角相等,那么一对对顶角也互补 |
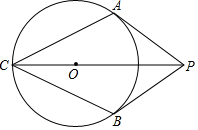 已知:如图,PA,PB是⊙O的切线,切点分别为A,B,连结PO并延长,交⊙O于点C,求证:AC=BC.
已知:如图,PA,PB是⊙O的切线,切点分别为A,B,连结PO并延长,交⊙O于点C,求证:AC=BC. 已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.
已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$. 如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于点H,若BC=5,AC=12,则AB=13,CH=$\frac{60}{13}$.
如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于点H,若BC=5,AC=12,则AB=13,CH=$\frac{60}{13}$.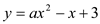 (
(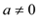 )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .