题目内容
 如图,在平面直角坐标系中,A、B、C三点的坐标分别为(3,0)、(1,
如图,在平面直角坐标系中,A、B、C三点的坐标分别为(3,0)、(1,| 3 |
考点:坐标与图形性质,三角形的面积
专题:
分析:根据三角形的面积公式,可得S△OAB、S△OBC,根据面积的和差,可得答案;
根据梯形的面积公式,可得四边形OABD,三角形的面积公式,可得S△BCD,根据面积的和差,可得答案.
根据梯形的面积公式,可得四边形OABD,三角形的面积公式,可得S△BCD,根据面积的和差,可得答案.
解答:解:解法一:如图1连接OB, ,
,
S四边形OABC=S△OAB+S△OBC=
×3×
+
×1×1=
;
解法二:如图2,作BD⊥y轴与D点, ,
,
S四边形OABC=四边形OABD-S△BCD=(1+3)×
÷2-
×(
-1)×1
=
-
=
.
 ,
,S四边形OABC=S△OAB+S△OBC=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
解法二:如图2,作BD⊥y轴与D点,
 ,
,S四边形OABC=四边形OABD-S△BCD=(1+3)×
| 3 |
| 1 |
| 2 |
| 3 |
=
4
| ||
| 2 |
| ||
| 2 |
=
3
| ||
| 2 |
点评:本题考查了坐标与图形,利用了图形的分割,图形的补充.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
下列各组数中,互为相反数的是( )
A、-3和
| ||
| B、-(-3)和+(+3) | ||
| C、+(-3)和-(+3) | ||
| D、-3和-(-3) |
如图所示,阴影部分面积最大的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC的长是( )
如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC的长是( )| A、2 | B、4 | C、6 | D、8 |
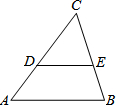 如图,DE∥AB,AC=3AD,S△ABC=5,则△CED的面积是
如图,DE∥AB,AC=3AD,S△ABC=5,则△CED的面积是 如图,A,B,C是⊙O的三等分点,A,D,E,F,G是⊙O的五等分点,求证:BE是⊙O的内接正十五边形的一边.
如图,A,B,C是⊙O的三等分点,A,D,E,F,G是⊙O的五等分点,求证:BE是⊙O的内接正十五边形的一边. 如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为
如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为