题目内容
11.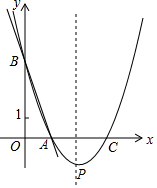 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=(x-h)2+k经过点A、B,其顶点为P.在抛物线的对称轴上是否存在一点Q,连接QA、QB,并将△ABQ沿AB翻折,得到菱形AQBQ′?若存在,请求出点Q的坐标;若不存在,说明理由.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=(x-h)2+k经过点A、B,其顶点为P.在抛物线的对称轴上是否存在一点Q,连接QA、QB,并将△ABQ沿AB翻折,得到菱形AQBQ′?若存在,请求出点Q的坐标;若不存在,说明理由.
分析 先求得点A、B的坐标,然后将点A和点B的坐标代入抛物线的解析式可求得h=2,由翻折的性质和菱形的判定定理可知当QB=QA时,四边形AQBQ′为菱形,设点Q的坐标为(2,a),由两点间的距离公式列出关于a的方程求解即可.
解答 解:如图所示:
把y=0代入直线y=-3x+3得:-3x+3=0,解得x=1,
∴A(1,0).
把x=0代入直线y=-3x+3得:y=3,
∴B(0,3).
将(1,0)、(0,3)代入抛物线的解析式得:$\left\{\begin{array}{l}{{h}^{2}+k=3}\\{(1-h)^{2}+k=0}\end{array}\right.$,解得:h=2,k=-1,
∴抛物线的对称轴为x=2.
由翻折的性质可知BQ′=BQ,AQ=AQ′.
∴当QB=QA时,四边形AQBQ′为菱形.
设点Q的坐标为(2,a),由两点间的距离公式可知:(2-1)2+a2=22+(3-a)2,解得a=2,
∴点Q的坐标为(2,2).
点评 本题主要考查的是二次函数与x轴的交点问题,判断出四边形AQBQ′为菱形的条件是解题的关键.

练习册系列答案
相关题目
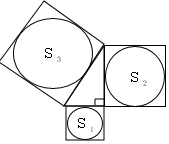 如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为S1,S2,S3,则S1,S2,S3之间的关系是S1+S2=S3.
如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为S1,S2,S3,则S1,S2,S3之间的关系是S1+S2=S3.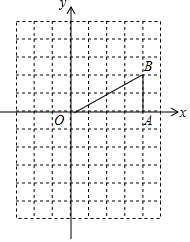 如图,在平面直角坐标系中,已知B(4,2),BA⊥x轴于A.
如图,在平面直角坐标系中,已知B(4,2),BA⊥x轴于A.