题目内容
1.如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上.(1)画出Rt△COD绕点O沿顺时针方向旋转60°后的图形;
(2)若将图中的△COD绕点O按每秒60°的速度沿顺时针方向旋转一周,在旋转的过程中,在$\frac{5}{3}$或$\frac{14}{3}$秒时,边CD恰好与边AB平行.
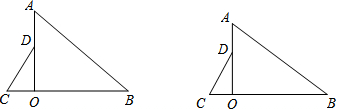
分析 (1)根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
(2)先作出图形,分两种情况:①两三角形在点O的同侧时,设CD与OB相交于点E,根据两直线平行,同位角相等可得∠CEO=∠B,根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE,然后求出旋转角∠AOD,再根据每秒旋转60°列式计算即可得解;②两三角形在点O的异侧时,延长BO与CD相交于点E,根据两直线平行,内错角相等可得∠CEO=∠B,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE,然后求出旋转角度数,再根据每秒旋转60°列式计算即可得解.
解答 解:(1)如图所示,△C'OD'是△COD绕点O沿顺时针方向旋转60°后的图形;
(2)分两种情况:
①两三角形在点O的同侧时,如图1,设CD与OB相交于点E,
∵AB∥CD,
∴∠CEO=∠B=40°,
∵∠C=60°,∠COD=90°,
∴∠D=90°-60°=30°,
∴∠DOE=∠CEO-∠D=40°-30°=10°,
∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°,
∵每秒旋转60°,
∴时间为100°÷60°=$\frac{5}{3}$秒;
②两三角形在点O的异侧时,如图2,延长BO与CD相交于点E,
∵AB∥CD,
∴∠CEO=∠B=40°,
∵∠C=60°,∠COD=90°,
∴∠D=90°-60°=30°,
∴∠DOE=∠CEO-∠D=40°-30°=10°,
∴旋转角为270°+10°=280°,
∵每秒旋转60°,
∴时间为280°÷60°=$\frac{14}{3}$秒;
综上所述,在第$\frac{5}{3}$或$\frac{14}{3}$秒时,边CD恰好与边AB平行.
故答案为:$\frac{5}{3}$或$\frac{14}{3}$.
点评 本题考查了旋转图形的作法,平行线的性质,旋转的性质以及三角形外角性质的运用,难点在于分情况讨论,解题时作出图形更形象直观.

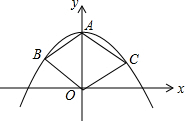 如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过菱形ABOC的三个顶点A、B、C,∠BAC=120°,则ac的值是-$\frac{2}{3}$.
如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过菱形ABOC的三个顶点A、B、C,∠BAC=120°,则ac的值是-$\frac{2}{3}$.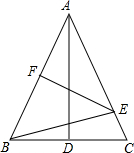 如图,AD和EF分别是△ABC中BC与AB垂直平分线,且BE+CE=20cm,则AB=20cm.
如图,AD和EF分别是△ABC中BC与AB垂直平分线,且BE+CE=20cm,则AB=20cm.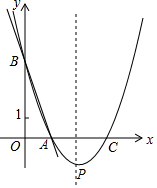 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=(x-h)2+k经过点A、B,其顶点为P.在抛物线的对称轴上是否存在一点Q,连接QA、QB,并将△ABQ沿AB翻折,得到菱形AQBQ′?若存在,请求出点Q的坐标;若不存在,说明理由.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=(x-h)2+k经过点A、B,其顶点为P.在抛物线的对称轴上是否存在一点Q,连接QA、QB,并将△ABQ沿AB翻折,得到菱形AQBQ′?若存在,请求出点Q的坐标;若不存在,说明理由.