题目内容
11. 如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最小值为8cm.
如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最小值为8cm.
分析 连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.
解答  解:连接AD,
解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×AD=12,解得AD=6cm,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+$\frac{1}{2}$BC=6+$\frac{1}{2}$×4=6+2=8cm.
故答案为:8.
点评 本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
16.甲看乙的方向是北偏东30°,则乙看甲的方向是( )
| A. | 南偏东60° | B. | 南偏东30° | C. | 南偏西60° | D. | 南偏西30° |
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.星星果汁店中的A种果汁比B种果汁每杯贵1元,小彬和同学买了3杯B种果汁,2杯A种果汁,一共花了16元,A种果汁B种果汁每杯分别多少元?设A种果汁的单价为x元,B种果汁的单价为y元,则以下方程组正确的是( )
| A. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y-1}\end{array}\right.$ |
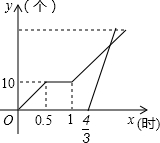 某车间甲、乙两名工人加工相同数量的相同零件,甲因特殊原因中间休息一段时间,重新开始工作后按原来的工作效率继续加工,乙因迟到,为了尽快完成任务,以甲3倍的工作效率加工,直到任务结束.如图是他们分别加工零件的数量y(个)与工作时间x(时)的函数图象
某车间甲、乙两名工人加工相同数量的相同零件,甲因特殊原因中间休息一段时间,重新开始工作后按原来的工作效率继续加工,乙因迟到,为了尽快完成任务,以甲3倍的工作效率加工,直到任务结束.如图是他们分别加工零件的数量y(个)与工作时间x(时)的函数图象



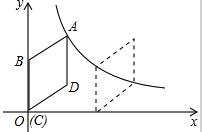 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.