题目内容
15.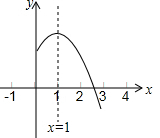 二次函数y=ax2+bx+c的图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法正确的是①②(填正确结论的序号).
二次函数y=ax2+bx+c的图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法正确的是①②(填正确结论的序号).①abc<0;②a-b+c<0;③2a+b<0;④当-1<x<3时,y>0.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①∵抛物线的开口向下,
∴a<0.
∵抛物线交y轴的正半轴,
∴c>0.
∵x=-$\frac{b}{2a}$=1,
∴a、b异号.
∴b>0.
∴abc<0故①正确.
②由抛物线的对称性可知当x=-1时,y<0,即a-b+c<0,故②正确;
③∵x=-$\frac{b}{2a}$=1,
∴2a+b=0,故③错误.
由函数图象可知:④错误.
故答案为:①②.
点评 本题主要考查对二次函数图象与系数的关系,抛物线与x轴的交点,二次函数图象上点的坐标特征等知识点的理解和掌握.熟练掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列运算正确的是( )
| A. | 3a3+4a3=7a6 | B. | 3a2-4a2=-a2 | C. | 3a2•4a3=12a3 | D. | (3a3)2÷4a3=$\frac{3}{4}$a2 |
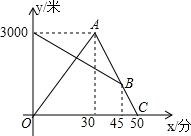 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,则下列说法:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,则下列说法: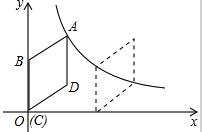 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.