题目内容
11.已知:正方形ABCD,点E在边CD上,点F在线段BE的延长线上,且∠FCE=∠CBE.(1)如图1,当点E为CD边的中点时,求证:CF=2EF;
(2)如图2,当点F位于线段AD的延长线上,求证:$\frac{EF}{BE}$=$\frac{DE}{DF}$.
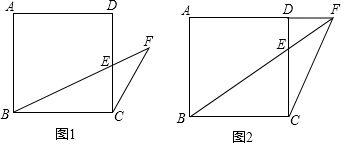
分析 (1)根据正方形的性质得到CD=BC,由点E为CD边的中点,得到CE=$\frac{1}{2}$CD=$\frac{1}{2}$BC,根据相似三角形的性质即可得到结论;
(2)根据正方形的性质得到DE∥AB,AD∥BC,AD=CD,根据平行线分线段成比例定理得到$\frac{EF}{BE}$=$\frac{DF}{AD}$,等量代换得到$\frac{EF}{BE}=\frac{DF}{CD}$,①根据相似三角形的性质得到$\frac{DE}{DF}$=$\frac{DF}{CD}$②,于是得到结论.
解答 (1)证明:∵四边形ABCD是正方形,∴CD=BC,
∵点E为CD边的中点,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$BC,
∵∠FCD=∠CBE,∠F=∠F,
∴△FCE∽△FBC,
∴$\frac{EF}{CF}=\frac{CE}{BC}$,
又∵CE=$\frac{1}{2}$BC,
∴$\frac{EF}{CF}$=$\frac{1}{2}$.
即CF=2EF;
(2)∵四边形ABCD是正方形,
∴DE∥AB,AD∥BC,AD=CD,
∵点F位于线段AD的延长线上,DE∥AB,
∴$\frac{EF}{BE}$=$\frac{DF}{AD}$,
又∵AD=CD,
∴$\frac{EF}{BE}=\frac{DF}{CD}$,①
∵AF∥BC,
∴∠DFE=∠CBE.
又∵∠DCF=∠CBE,
∴∠DFE=∠DCF,
又∵∠FDE=∠CDF,
∴△FDE∽△CDF,
∴$\frac{DE}{DF}$=$\frac{DF}{CD}$②,
由①②得,$\frac{EF}{BE}$=$\frac{DE}{DF}$.
点评 本题考查了相似三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

| A. | a>-1 | B. | a≥-1 | C. | a<-1 | D. | a≤-1 |

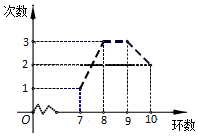 一名射击运动员连续打靶9次,假如他打靶命中环数的情况如图所示,那么该射击运动员本次打靶命中环数的中位数为9环.
一名射击运动员连续打靶9次,假如他打靶命中环数的情况如图所示,那么该射击运动员本次打靶命中环数的中位数为9环. 如图,在正方形ABCD中,点E、F分别在边BC、CD上,△AEF是等边三角形,如果AB=1,那么CE的长是$\sqrt{3}$-1.
如图,在正方形ABCD中,点E、F分别在边BC、CD上,△AEF是等边三角形,如果AB=1,那么CE的长是$\sqrt{3}$-1.