题目内容
1.已知方程组$\left\{\begin{array}{l}{a+2b=6}\\{3a-b=4}\end{array}\right.$.(1)求关于x的方程ax2+5x-3=0的实数根;
(2)求$\frac{{a}^{2}-{b}^{2}}{2a+2b}$+$\frac{3b-2a}{4a+b}$的值.
分析 (1)直接解方程组进而得出a,b的值,再代入方程求出答案;
(2)首先将分式化简,进而代入a,b的值求出答案.
解答 解:$\left\{\begin{array}{l}{a+2b=6①}\\{3a-b=4②}\end{array}\right.$,
①+②×2得:
7a=14,
解得:a=2,
则b=2,
故方程组的解为:$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$,
(1)关于x的方程ax2+5x-3=0为:2x2+5x-3=0
(x+3)(2x-1)=0,
解得:x1=-3,x2=$\frac{1}{2}$;
(2)$\frac{{a}^{2}-{b}^{2}}{2a+2b}$+$\frac{3b-2a}{4a+b}$
=$\frac{(a+b)(a-b)}{2(a+b)}$+$\frac{3b-2a}{4a+b}$
=$\frac{a-b}{2}$+$\frac{3b-2a}{4a+b}$
把a,b的值代入得:
原式=0+$\frac{6-4}{8+2}$=$\frac{1}{5}$.
点评 此题主要考查了一元二次方程的解法以及分式的化简、二元一次方程的解法等知识,正确得出a,b的值是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列各有理式中,为分式的是( )
| A. | $\frac{x}{3x-1}$ | B. | -$\frac{{x}^{2}+1}{2}$ | C. | $\frac{\sqrt{5y}}{x}$ | D. | $\frac{(x+2)(x-2)}{π}$ |
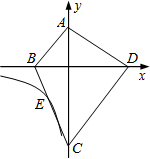 如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )
如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )