题目内容
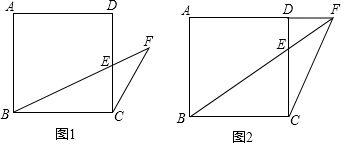
16. 如图,在正方形ABCD中,点E、F分别在边BC、CD上,△AEF是等边三角形,如果AB=1,那么CE的长是$\sqrt{3}$-1.
如图,在正方形ABCD中,点E、F分别在边BC、CD上,△AEF是等边三角形,如果AB=1,那么CE的长是$\sqrt{3}$-1.
分析 由于四边形ABCD是正方形,△AEF是等边三角形,所以首先根据已知条件可以证明△ABE≌△ADF,再根据全等三角形的性质得到BE=DF,设BE=x,那么DF=x,CE=CF=1-x,那么在Rt△ABE和Rt△ADF利用勾股定理可以列出关于x的方程,解方程即可求出BE.
解答 解:∵四边形正方形ABCD,
∴∠B=∠D=90°,AB=AD,
∵△AEF是等边三角形,
∴AE=EF=AF,
∴△ABE≌△ADF,
∴BE=DF,
设BE=x,那么DF=x,CE=CF=1-x,
在Rt△ABE中,AE2=AB2+BE2,
在Rt△EFC中,FE2=CF2+CE2,
∴AB2+BE2=CF2+CE2,
∴x2+1=2(1-x)2,
∴x2-4x+1=0,
∴x=2±$\sqrt{3}$,而x<1,
∴x=2-$\sqrt{3}$,
即BE的长为=2-$\sqrt{3}$,
∴CE=BC-BE=1-(2-$\sqrt{3}$)=$\sqrt{3}$-1.
点评 本题主要考查了正方形、等边三角形的知识,把求线段长放在正方形的背景中,利用勾股定理列出一元二次方程解决问题,难度适中.

练习册系列答案
相关题目
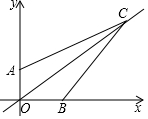 如图,已知点A(0,3),B(4,0),点C在第一象限,且AC=5$\sqrt{5}$,BC=10,则直线OC的函数表达式为y=$\frac{4}{5}$x.
如图,已知点A(0,3),B(4,0),点C在第一象限,且AC=5$\sqrt{5}$,BC=10,则直线OC的函数表达式为y=$\frac{4}{5}$x.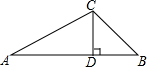 南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)
南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)