题目内容
17.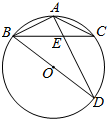 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.(1)判断△ABE与△ADB是否相似,并说明理由;
(2)求AB的长;
(3)求∠C的正切值.
分析 (1)根据AB=AC,那么弧AB=弧AC,根据圆周角定理即可得出结论.
(2)可通过相似三角形得出线段成比例,然后求长度,(1)中已得出∠ABC=∠ADB,那么三角形ABE,ABE就相似(有一个公共角).可得出关于AE、AB、AD的关系式,有AE的长,有AD的长,那么就能求出AB的长了.
(3)可从角的度数入手,根据(2)中得出的数据不难求出∠D的度数,也就求出了∠ABD、∠ACB、∠ABC的度数,于是得到结论.
解答 解:(1)△ABE与△ADB相似,
理由:∵AB=AC,
∴∠ABC=∠ACB.
∴弧AB=弧AC.
∴∠ABC=∠ADB,
∵∠BAE=∠DAB,
∴△ABE∽△ADB;
(2)解:∵∠ABE=∠ADB,∠BAE=∠BAD,
∴△ABE∽△ADB.
∴$\frac{AE}{AB}$=$\frac{AB}{AD}$.
∵AE=2,AD=AE+ED=2+4=6,
∴$\frac{2}{AB}=\frac{AB}{6}$,
∴AB=2$\sqrt{3}$;
(3)解:AC∥BD.理由如下:
∵BD为⊙O的直径,
∴∠BAD=90°.
∵AB=2$\sqrt{3}$,AD=6,
∴在Rt△BAD中,tan∠BDA=$\frac{AB}{AD}$=$\frac{\sqrt{3}}{3}$.
∵∠ACB=∠BDA,
∴tan∠C=$\frac{\sqrt{3}}{3}$.
点评 本题考查了相似三角形的判定和性质,圆周角定理.三角函数的定义,熟练正确相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
5.如图图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.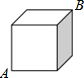 如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
 如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )| A. | 3 | B. | $\sqrt{2}+1$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
2.一元二次方程x2=3x的根是( )
| A. | 0 | B. | 3 | C. | 0和3 | D. | 0和-3 |

 一个正方体的表面展开图如图所示,则原正方体中的“★”所在面的对面所标的字是田.
一个正方体的表面展开图如图所示,则原正方体中的“★”所在面的对面所标的字是田. 画图题
画图题