题目内容
1．
已知：AB∥CD，EF∥CD，且∠ABC=20°，∠CFE=30°，则∠BCF的度数是50°．
分析 根据平行线的性质，由AB∥CD得∠BCD=∠ABC=20°，由EF∥CD得∠DCF=∠CFE=30°，然后利用∠BCF=∠BCD+∠DCF进行计算即可．
解答 解：∵AB∥CD，
∴∠BCD=∠ABC=20°，
∵EF∥CD，
∴∠DCF=∠CFE=30°，
∴∠BCF=∠BCD+∠DCF=50°．
故答案为50°．
点评 本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
相关题目
11．有五张形状、大小、质地都相同的卡片，上面分别画有下列图形：①线段，②等边三角形，③平行四边形，④直角三角形，⑤菱形．若将卡片背面朝上并洗匀，则从中任意抽取一张，正面图形既是轴对称图形，又是中心对称图形的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
矩形ABCD中，E在CD上，将△ADE沿AE折叠，使点D落在边BC上的F处，如果∠EAD=15°，则∠BAF为60°．
9．
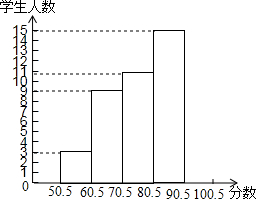为了了解奥运知识，某中学举行了一次“奥运知识竞赛”，共有900名学生参加了这次竞赛，为了了解本次竞赛情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分），进行统计，请你根据下面尚未完成的统计表和统计图，解答下列问题．
（1）根据以上信息，统计表中A=0.18，B=12，C=0.24；
（2）补全统计图；
（3）在该问题中，个体是每一个学生的竞赛成绩；
（4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
为了了解奥运知识，某中学举行了一次“奥运知识竞赛”，共有900名学生参加了这次竞赛，为了了解本次竞赛情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分），进行统计，请你根据下面尚未完成的统计表和统计图，解答下列问题．| 分组 | 频数 | 频率 |
| 50.5～60.5 | 3 | 0.06 |
| 60.5～70.5 | 9 | A |
| 70.5～80.5 | 11 | 0.22 |
| 80.5～90.5 | 15 | 0.30 |
| 90.5～100.5 | B | C |
（2）补全统计图；
（3）在该问题中，个体是每一个学生的竞赛成绩；
（4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
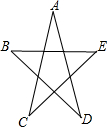如图，∠A+∠B+∠C+∠D+∠E的度数是180°．
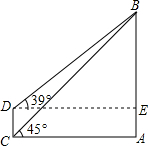目前世界上最高的电视塔是广州新电视塔．如图所示，新电视塔高AB为610米，远处有一栋大楼，某人在楼底C处测得塔顶B的仰角为45°，在楼顶D处测得塔顶B的仰角为39°，（sin39°≈0.63，cos39°≈0.78，tan39°≈0.81）
如图，在矩形ABCD中，以B为圆心，BC长为半径作弧，交AD于E，连接BE，过C点作CF⊥BE于F．
11．
如图，已知△ACD∽△BCA，若CD=4，AC=6，则BC等于（ ）
如图，已知△ACD∽△BCA，若CD=4，AC=6，则BC等于（ ）| A． | 9 | B． | 10 | C． | 11 | D． | 12 |