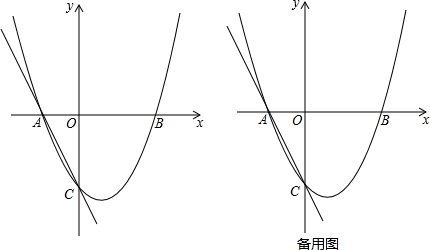
题目内容
9.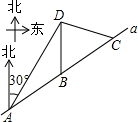 如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30°方向12km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=4$\sqrt{3}$km.
如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30°方向12km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=4$\sqrt{3}$km.(1)现准备由景点D向公路a修建一条距离最短的公路,不考虑其他因素,求出这条公路的长;
(2)求出景点B与景点C之间的距离(结果保留根号).
分析 (1)过点D作DE⊥AC于点E,过点A作AF⊥DB,交DB的延长线于点F,求DE的问题就可以转化为求∠DBE的度数或三角函数值的问题.
(2)Rt△DCE中根据三角函数就可以求出BE,CE的长,即可解决问题.
解答 解:(1)如图,过点D作DE⊥AC于点E,
过点A作AF⊥DB,交DB的延长线于点F,
在Rt△DAF中,∠ADF=30°,
∴AF=$\frac{1}{2}$AD=$\frac{1}{2}$×12=6,
∴DF=$\sqrt{A{D}^{2}-A{F}^{2}}$=6 $\sqrt{3}$,
在Rt△ABF中BF=$\sqrt{A{B}^{2}-A{F}^{2}}$=2$\sqrt{3}$,
∴BD=DF-BF=6$\sqrt{3}$-2$\sqrt{3}$=4$\sqrt{3}$,
sin∠ABF=$\frac{AF}{AB}$=$\frac{6}{4\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,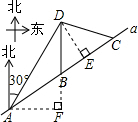
∴∠ABF=∠DBE=60°,
在Rt△DBE中,DE=BD•sin60°=6(km),
∴景点D向公路a修建的这条公路的长约是6km;
(2)由题意可知∠CDB=75°,
∴∠DCE=180°-60°-75°=45°,
∴DE=CE=6(km),BE=$\frac{1}{2}$BD=2$\sqrt{3}$
∴BC=BE+CE=2$\sqrt{3}$+6(km)
∴景点C与景点B之间的距离约为(2$\sqrt{3}$+6)km.
点评 本题主要考查解直角三角形问题,方位角等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
4.下列运算正确的是( )
| A. | a+a2=a3 | B. | (a2)3=a6 | C. | (x-y)2=x2-y2 | D. | a2a3=a6 |
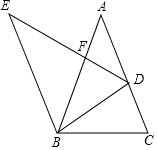 如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.
如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$. 某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)